Расчётчик всегда должен помнить, что все расчётные функции, реализованные в любом программном комплексе, имеют под собой теоретическую основу, поэтому тема сегодняшней заметки посвящается теории расчёта эквивалентных напряжений.
В расчетах на прочность при простых напряженных состояниях, в частности, при одноосном напряженном состоянии и состоянии чистого сдвига, задача является сравнительно простой, так как эти напряженные состояния воспроизводятся при испытаниях на растяжение и на кручение стержней. Об опасности действующих напряжений можно судить, сопоставляя их с экспериментально полученным пределом текучести для пластических материалов или с временным сопротивлением для хрупких. Но чаще напряженное состояние является сложным. Технически невозможно проводить испытания материалов при сложном напряженном состоянии из-за бесконечного числа этих напряженных состояний. Поэтому ученые мужи выбрали другой путь решения данной задачи: сведении сложного напряженного состояния к эквивалентному ему простому - одноосному и сравнение эквивалентного напряжения с предельным одноосным, определяемым экспериментально. При сведении сложного напряженного состояния к эквивалентному обычно используется некоторый критерий прочности – теории прочности, которые дают возможность находить эквивалентное напряженное состояние как функцию одного, двух или всех трех главных напряжений.
К сожалению, наука не смогла определить истинную причину разрушения материалов, поэтому единой общей теории прочности не существует, есть много разрозненных теорий, каждая из которых базируется на своем критерии разрушения материала.
Для удобства все теории, позволяющие произвести расчёт эквивалентных напряжений и их характеристик, реализованные в ЛИРА 10.6, сведены в таблицу 1.
| № п/п | Наименование теории прочности | Формула | Геометрическая интерпретация | Примечания |
1 | 2 | 3 | 4 | 5 |
1 | Наибольших главных напряжений | 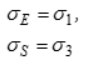
| Куб с центром, смещенным относительно начала координат в сторону гидростатического давления | Исторически первая теория прочности – предложенная Г. Галилеем. Удовлетворительно описывает предельное состояние весьма хрупких, достаточно однородных материалов, таких как стекло, гипс, некоторые виды керамики |
2 | Наибольших главных деформаций | 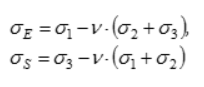
| Равносторонний косоугольный параллелепипед с осью симметрии, равнонаклоненной к координатным осям | Предложена Э. Мариоттом и развита Б. Сен-Венаном. Ввиду малой достоверности в настоящее время почти не применяется |
3 | Наибольших касательных напряжений | 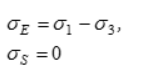
| Правильная шестигранная призма, равно наклоненная к осям координат | Предложена Ш. Кулоном. Удовлетворительно описывает предельное состояние пластичных малоупрочняющихся материалов (отпущенные стали), для которых характерна локализация пластических деформаций |
4 | Энергетическая | 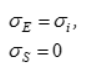
| Круговой цилиндр, описанный вокруг призмы, интерпретирующей теорию максимальных касательных напряжений | Предложена М.Губером, Г. Генки, Р.Мизесом. Хорошо описывает предельное состояние широкого класса пластичных материалов (медь, никель, алюминий, углеродистые и хромоникелевые стали) |
5 | Теория О. Мора | 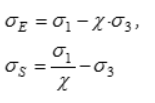
| Шестигранная равнонаклоненная к осям пирамида | Применяется для установления предельного состояния достаточно однородных материалов, по разному сопротивляющихся растяжению и сжатию |
6 | Друккера – Прагера | 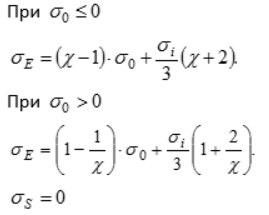
| Двуполостной параболоид вращения, равнонаклоненный к осям координат | Удовлетворительно описывает предельное состояние сравнительно пластичных материалов, для которых параметр 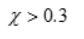
|
7 | Писаренко – Лебедева | 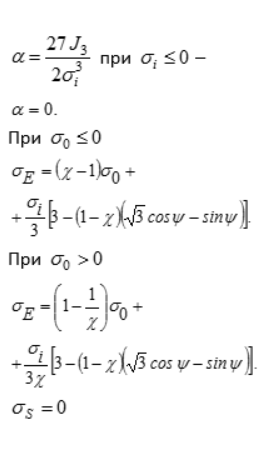 | Коническая поверхность, описанная вокруг пирамиды Мора. В сечении октаэдрической плоскостью – равносторонний криволинейный треугольник | Хорошо описывает предельное состояние широкого класса достаточно однородных конструкционных материалов. При 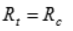 преобразуется в энергетическую теорию. В случае, когда преобразуется в энергетическую теорию. В случае, когда 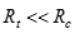 (весьма хрупкие материалы), результаты вычислений практически совпадают с данными расчета по теории наибольших главных напряжений (весьма хрупкие материалы), результаты вычислений практически совпадают с данными расчета по теории наибольших главных напряжений |
8 | Гениева | 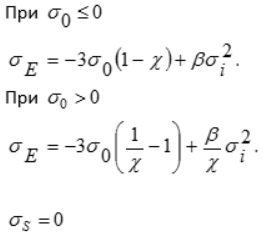
| — | Хорошо описывает предельное состояние бетона |
9 | Кулона – Мора | 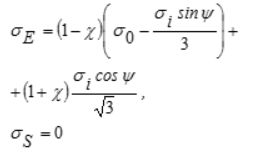
| — | Грунт |
10 | Боткина | 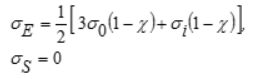
| — | Грунт |
Условные обозначения
σ
E - эквивалентное напряжение при растяжении;
σ
S - эквивалентное напряжение при сжатии;
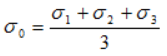
- среднее напряжение
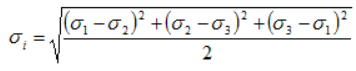
- интенсивность напряжений
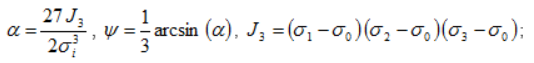 Rt, Rc
Rt, Rc - предельные напряжения растяжения и сжатия, для грунтов
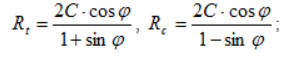 С
С - сцепление;
φ - угол внутреннего трения;
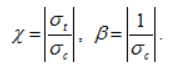
Стоит отметить, что описанные выше теории расчёта эквивалентных напряжений реализованы в ЛИРА 10.6 для пластинчатых и объемных элементов, узнать о расчете напряжений в стержнях можно в соответствующей заметке.
Использованная литература:
- Писаренко Г. С. Справочник по сопротивлению материалов / Г. С. Писаренко, А. П. Яковлев, В. В. Матвеев.: Наукова думка, 1988. – 736 с.