Содержание:
- Исходные данные
- Задача
- Построение расчетной модели
- Статический расчет
- Поверочный расчет кладки на внецентренное сжатие
- Расчет стен на вертикальную нагрузку по раскрытию трещин
- Автоматизация поверочного расчета кладки на внецентренное сжатие
Несмотря на повсеместное применение при массовом жилищном строительстве зданий с полным монолитным железобетонным каркасом или зданий с панельной несущей системой, все еще остаются актуальны бескаркасные здания с несущими каменными стенами. Так ранее широко были распространены здания типовых серий – 511, 85, 86, 528, 51, 477 и многие другие, конструктивные схемы данных зданий были подробно исследованы, были разработаны аналитические методики для расчета.
Но современное развитие девелопмента, привело к тому, что сейчас почти каждое кирпичное здание является нетиповым. Застройщики стремятся адаптировать планировки и квартирографию под быстро меняющиеся запросы клиента. С учетом конкурентного рынка происходит значительная экономия материалов, уменьшается толщина несущих стен, увеличиваются пролеты плит перекрытий - данные дополнительные требования усложняют конструктивные решения, усложняют анализ проектируемых зданий и ранее применяемые для расчета зданий методики оказываются трудоемкими для нахождения усилий и конструирования элементов, тем более, с учетом изменчивой жесткости грунтового основания. Для решения этой задачи инженер-конструктор может использовать аппарат современных расчетных комплексов, основанных на применении метода конечных элементов (МКЭ), такого как ЛИРА 10. В данной заметке продемонстрирован один из возможных сценариев расчета бескаркасных зданий с кирпичными несущими стенами.
Исходные данные:
Двухподъездная секция жилого 6-этажного дома. Несущие стены - толщиной 380мм из кирпича СУРПо-M200/F75/2.0 на растворе М100. Цокольная часть - из кирпича КОРПо 1НФ/150/75/2,0 на растворе М100. Несущие стены рассматриваем как неармированные. Стены подвала - из блоков ФБС. Фундамент – ленточный на естественном основании из бетона В20. Перекрытия – плиты пустотные ПБ (безопалубочного формования) толщиной 220мм. Строительство в г. Москва.
Задача:
Выполнить поверочный расчет несущих стен с учетом требований СП 15.13330.2020 «Каменные и армокаменные конструкции. Актуализированная редакция СНиП II-22-81*».
Построение расчетной модели:
Исходную 3D модель здания строим с применением программного комплекса Tekla Structures. Так как при поверочном расчете в СП 15.13330.2020 «Каменные и армокаменные конструкции. Актуализированная редакция СНиП II-22-81*» (далее по тексту - [1]) рассматривается анализ отдельных простенков, то предварительно также автоматически формируем их в BIM программе.
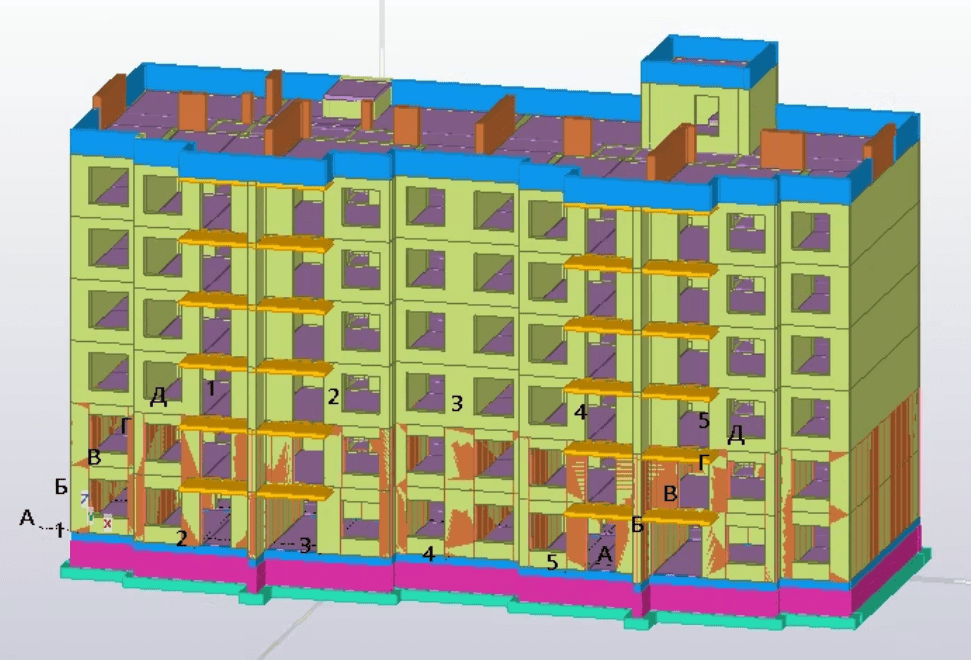
Рисунок 1. Исходная 3D модель в Tekla Structures
Импортируем 3D модель в ЛИРА 10. Программа имеет обширный перечень связок с современными BIM программами, в которых возможно на основе архитектурной модели построить конструктивную модель, наделить ее всеми необходимыми свойствами и передать далее на расчет в ЛИРА 10. В процессе вставки возможен импорт геометрии, нагрузок, материалов, граничных условий.

Рисунок 2. Расчетная модель в ЛИРА 10. «Архитектурные элементы»
Выполняем триангуляцию модели, назначаем граничные условия (условия сопряжения элементов, грунтовые условия и т.д.). Необходимо отметить, что предварительно были созданы расчетные простенки в виде стержневых элементов, данные простенки являются эквивалентными стержнями и не участвуют в построении матрицы жесткости, а служат для автоматического сбора усилий с пластинчатых элементов. Данная функция позволяет значительно ускорить процесс сбора усилий в простенках для последующих проверок согласно [1].
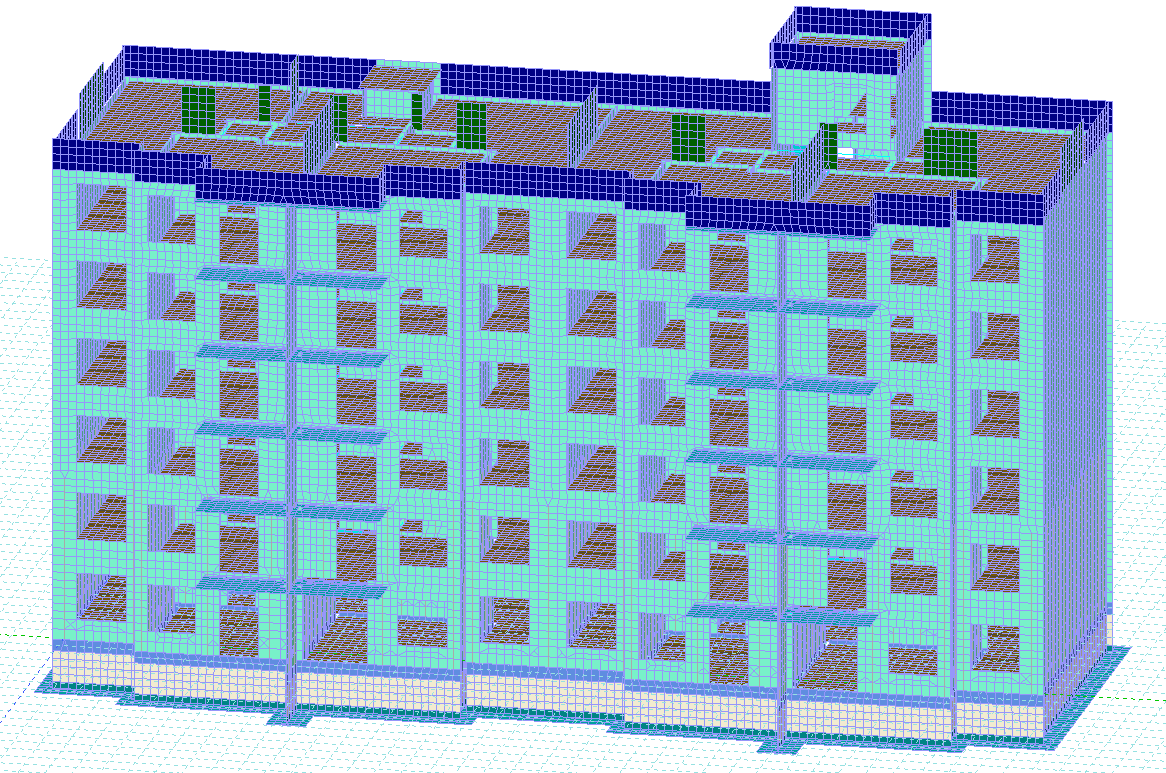
Рисунок 3. Конечно-элементная модель в ЛИРА 10.
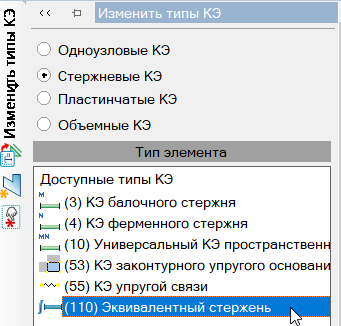
Рисунок 4. Назначение эквивалентным стержням соответствующего типа КЭ.
Для объединения отдельных сетей стен, плит перекрытий возможно использовать функцию «согласование сетей», данная функция позволяет создать автоматические связи между сетями даже не имеющих общих узлов. Для плит возможно задать шарнирное опирание, что отвечает фактическому закреплению.
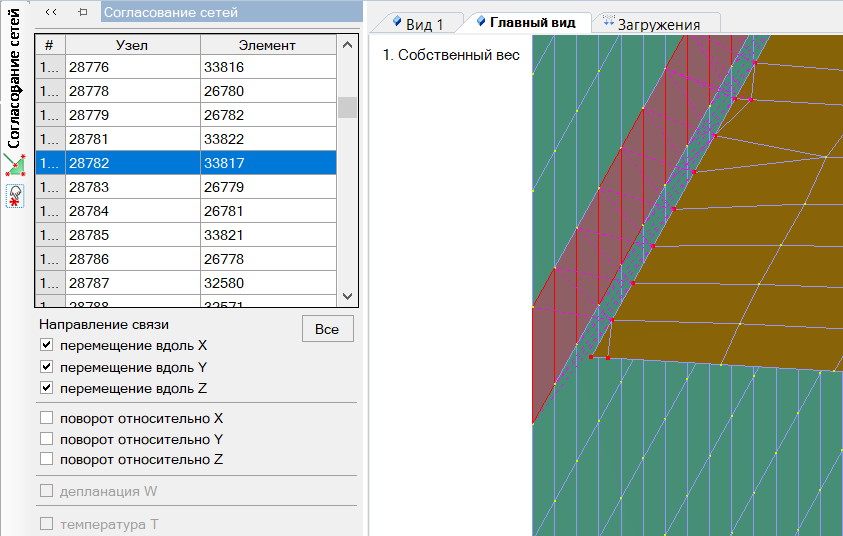
Рисунок 5. Шарнирный узел опирания плит перекрытия на стену, согласование сетей
Далее прикладываем действующие нагрузки на расчетную схему – собственный вес конструкций, эксплуатационные нагрузки, нагрузки от перегородок, ветровые нагрузки, снеговые нагрузки, нагрузки от грунта на подземную часть.
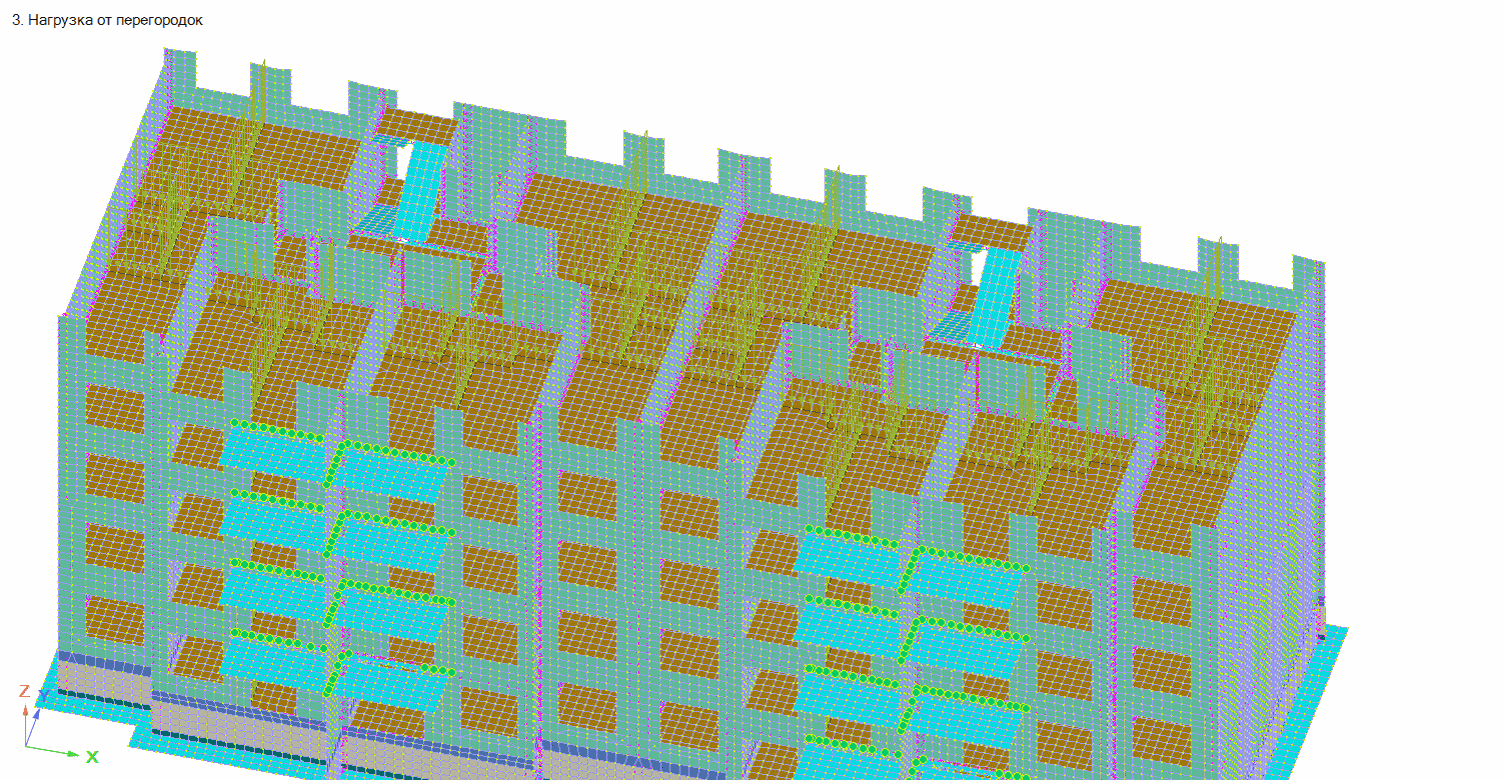
Рисунок 6. Загружение расчетной схемы. Нагрузка от перегородок.
Ветровую нагрузку задаем с помощью специальной функции «Ветровая нагрузка», которая производит автоматическое вычисление величины нагрузки и приложение ее на произвольную поверхность.
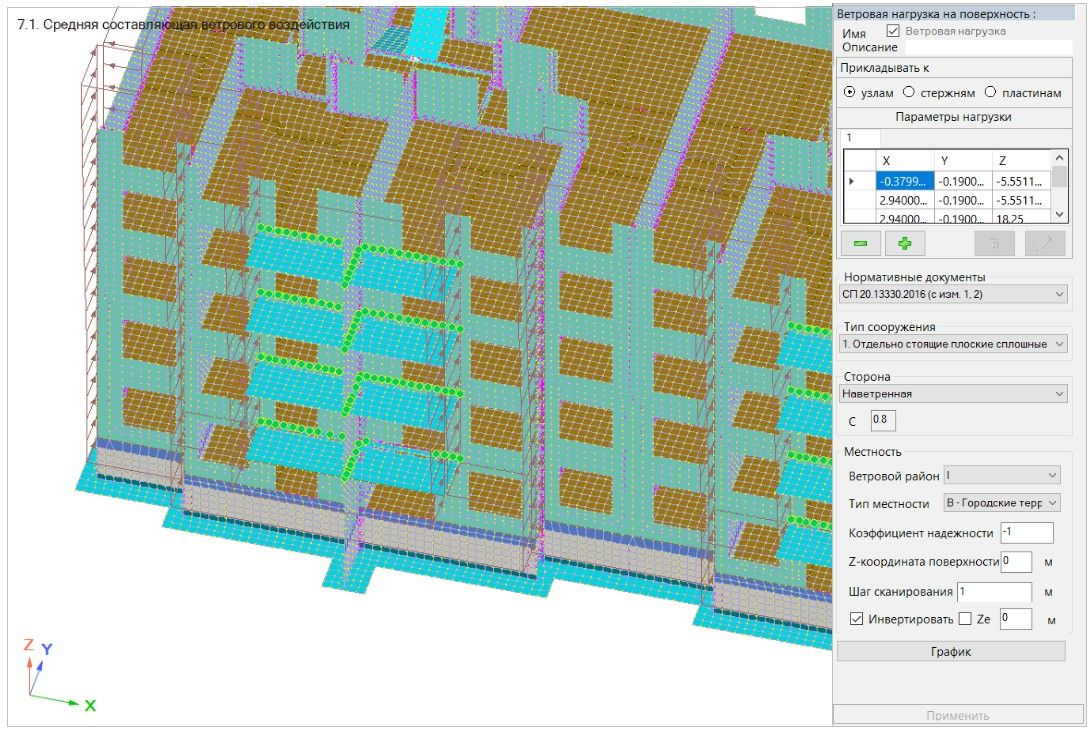
Рисунок 7. Загружение расчетной схемы. Ветровая нагрузка.

Рисунок 8. Список загружений расчетной модели
На следующем шаге нам необходимо определить параметры применяемых материалов и назначить их элементам модели.
Для того, чтобы определить жесткости материалов воспользуемся основными положениями [1] и вычислим основные параметры необходимые для дальнейшего расчета. Вычисления произведем для кладки из кирпича марки СУРПО-M200/F75/2.0 на растворе М100, для остальных материалов вычисления производятся аналогично.
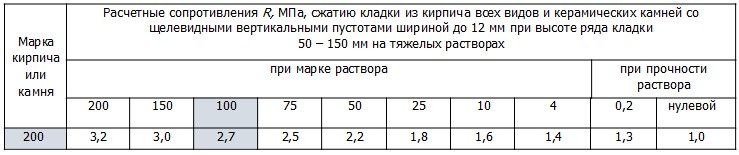
Согласно п.п. 6.2 [1] - Расчетные сопротивления R сжатию кладки на тяжелых растворах из кирпича всех видов и керамических камней со щелевидными вертикальными пустотами шириной до 12 мм, пустотностью до 27 % при высоте ряда кладки 50 – 150 мм на тяжелых растворах принимаются по таблице 2. Принятые значения для расчета выделены цветом.
Таблица 2 [1]
При дальнейшем расчете также необходимо учесть требования п.п 6.12 [1], а именно: расчетные сопротивления кладки сжатию, приведенные в таблицах 2 – 10, следует умножать на коэффициенты условий работы γс, равные:
а) 0,8 – для столбов и простенков площадью сечения 0,3 м2 и менее;
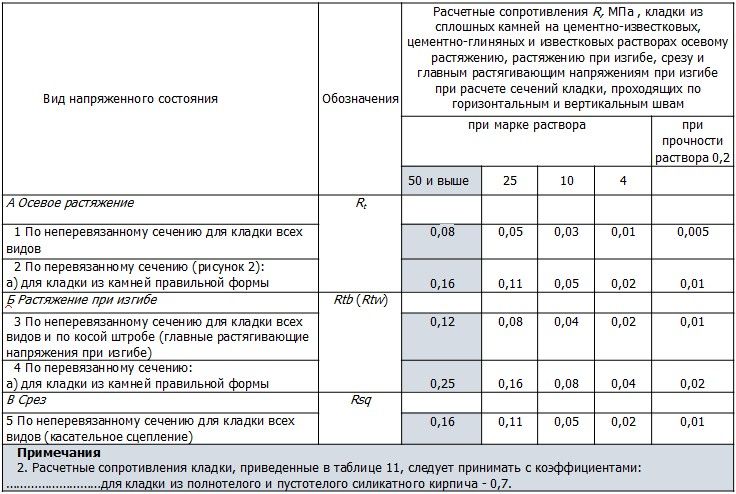
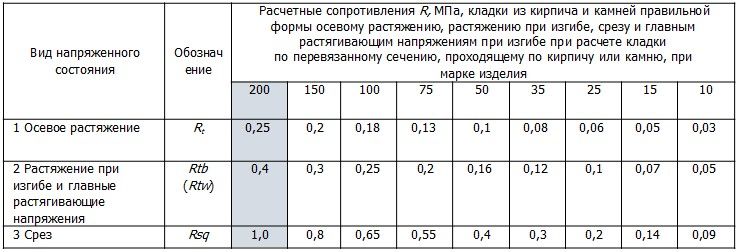
Расчетные характеристики кладки на растяжение определяем согласно п.п. 6.16 [1]: расчетные сопротивления кладки из сплошных камней на цементно-известковых, цементно-глиняных и известковых растворах осевому растяжению Rt, растяжению при изгибе Rtb и главным растягивающим напряжениям при изгибе Rtw, срезу Rsq при расчете сечений кладки, проходящих по горизонтальным и вертикальным швам, приведены в таблице 11.
Таблица 11 [1]
Расчетные сопротивления кладки на срез по перевязанному сечению принимаем по таблице 12 [1].
Таблица 12 [1]
Модуль упругости (начальный модуль деформаций) кладки при Е0 кратковременной нагрузке определяем согласно п.п. 6.21 [1], для неармированной кладки:
Е0 = αRu,
где α – упругая характеристика кладки, принимается по таблице 16;
Таблица 16 [1]

Ru – временное сопротивление (средний предел прочности) сжатию кладки, определяемое по формуле:
Ru = kR = 2 * 2.7 = 5.4 МПа,
где k – коэффициент, принимаемый по таблице 15; R – расчетные сопротивления сжатию кладки, принимаемые по таблицам 2–10 с учетом коэффициентов, приведенных в примечаниях к этим таблицам, а также в 6.10 – 6.15.
Таблица 15 [1]

Так как для рассматриваемого типа зданий в качестве основных нагрузок выступают нагрузки от собственного веса, то согласно п.п. 6.25 [1] модуль упругости кладки Е0 при постоянной и длительной нагрузке с учетом ползучести следует уменьшать путем деления его на коэффициент ползучести v=3,0 – для кладки из силикатного кирпича и камней полнотелых и пустотелых, а также из камней, изготовленных из бетона на пористых заполнителях и силикатных крупных блоков.
Итоговое значение модуля деформации для кладки из кирпича марки СУРПО-M200/F75/2.0 на растворе М100 для расчета принимаем равным:
Е0 = αRu / v = 750 * 5.4 / 3 = 1350 МПа
Согласно п.п. 6.28 [1] модуль сдвига кладки следует принимать равным:
G = 0,4 Е0 = 0.4 * 1350 = 540 Мпа
Статический расчет:
После задания всех необходимых характеристик расчетной модели производим статический расчет, определяем расчетные усилия. Далее представлены различные варианты визуализации внутренних усилий.
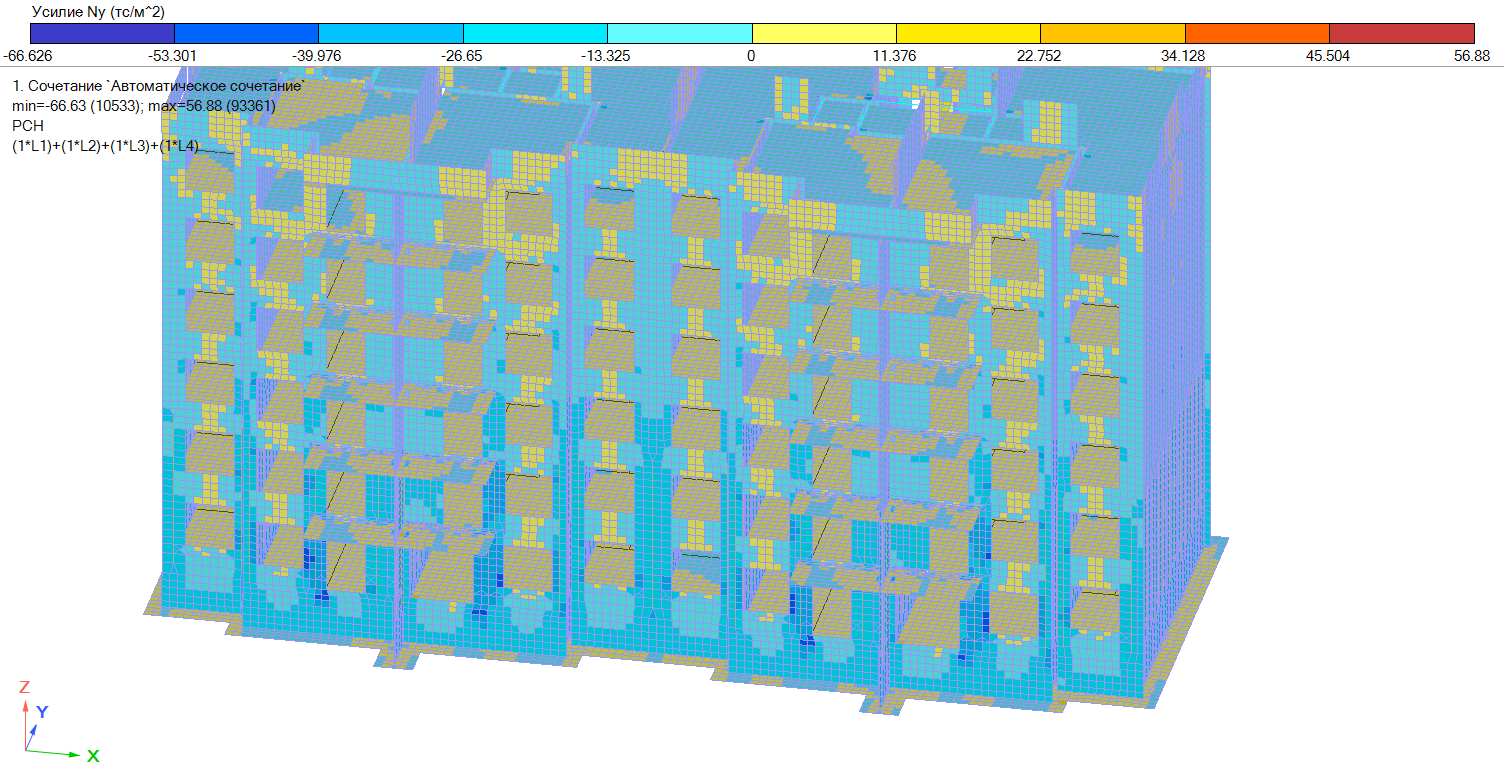
Рисунок 9. Мозаика напряжений Ny, т/м2
Усилия в простенках возможно посмотреть, как усилия в стержневых элементах, в том числе, продольные усилия, изгибающие моменты.
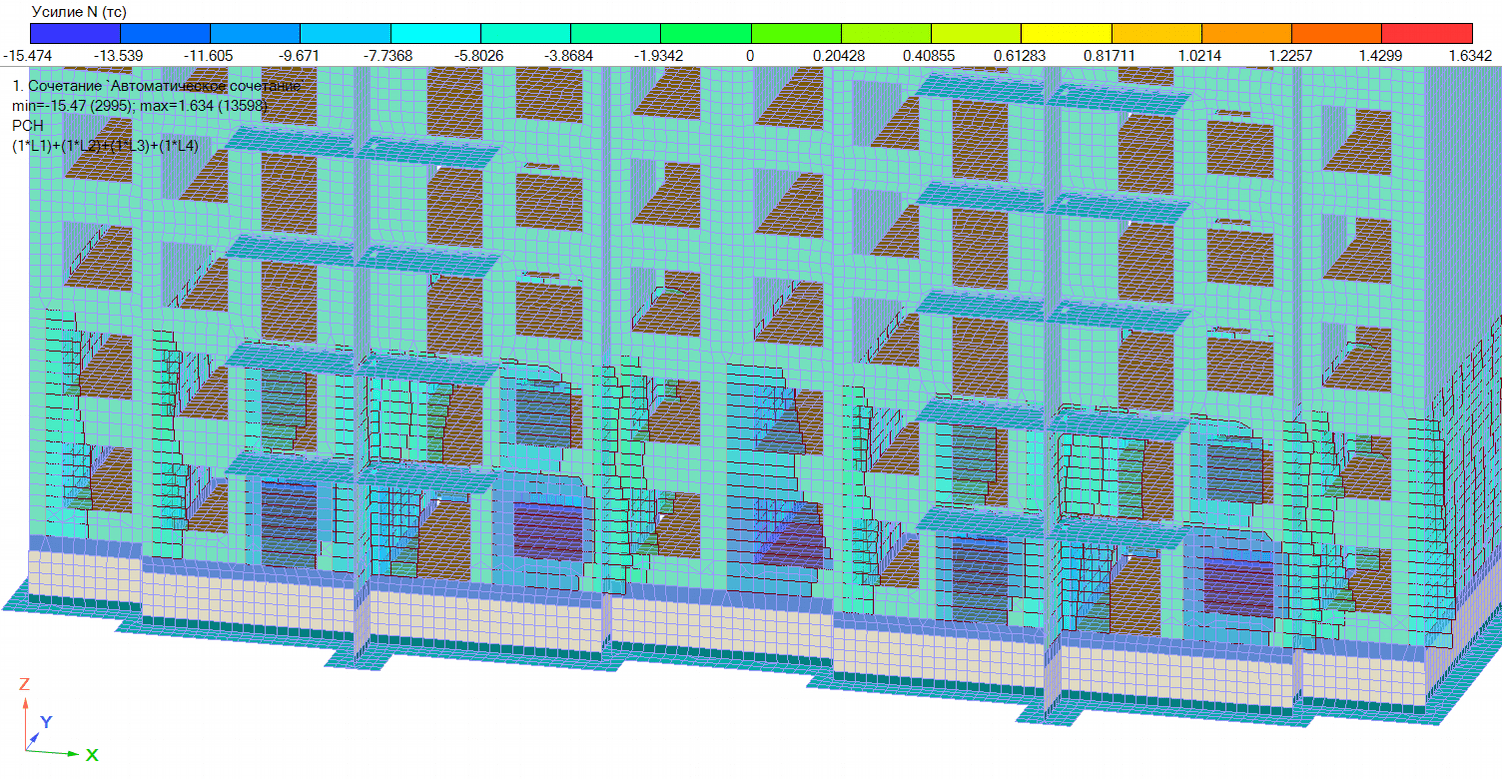
Рисунок 10. Эпюры продольных усилий в эквивалентных элементах, т
Концепция эквивалентных элементов основана на том, чтобы суммарные усилия в центре эквивалентного элемента соответствовали сумме узловых сил и моментов в элементе, с которых мы собираем усилия. Под узловыми силами и моментами здесь подразумеваются нагрузки, приводящие к возникновению напряжений в элементе. Для отдельного стержневого эквивалентного элемента в сбор усилий попадают те узлы, которые размещены между нормальными плоскостями, проходящими через два узла эквивалентного элемента. Для иллюстрации сбора нагрузки на эквивалентный элементный стержень произведем ручной сбор в сечении произвольного простенка.

Рисунок 11. Эпюры N, т. Мозаика напряжений Ny, т/м2
Выполним интегрирование в рассматриваемом сечении, определим продольную силу, действующую в эквивалентном стержне, и сравним значение с тем, которое автоматически определилось:
N = В (N1 l1+N2 l2+N3 l3+N4 l4) = -0.38*0.225(125.75+128.33+131.53+136.04) = -44.6 т
Сбор нагрузки произвелся корректно. Таким образом данный подход может быть использован при формировании расчетной схемы здания или сооружения, когда определенные элементы из-за их сложности необходимо замоделировать пластинчатыми или объемными элементам, а конструирование выполнить для стержневых или пластинчатых элементов, соответственно.
Поверочный расчет кладки на внецентренное сжатие:
Перед выполнением поверочного расчета всех простенков предварительно пройдем по основным этапам проверки согласно [1] и выполним проверку одного из простенков. Рассмотрим простенок №2886, для которого ранее определили усилия в эквивалентных стержнях, расчет производим на РСН 1, но для полного анализа несущей способности простенка необходимо выполнить расчет на все возможные сочетания нагрузок:
N = -44.6т; M=0.048т*м; Q=-0.007т.
Согласно п.п.7 [1] расчет внецентренно сжатых неармированных элементов каменных конструкций следует производить по формуле:
N ⩽ mg φ1 R Acω, (13)
где Ас – площадь сжатой части сечения при прямоугольной эпюре напряжений, определяемая из условия, что ее центр тяжести совпадает с точкой приложения расчетной продольной силы N. Положение границы площади Ас определяется из условия равенства нулю статического момента этой площади относительно ее центра тяжести для прямоугольного сечения.
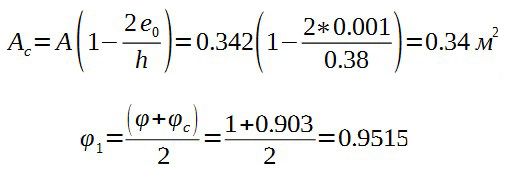
R – расчетное сопротивление кладки сжатию;
R=2.7 Мпа
А – площадь сечения элемента;
A = 0.38 * 0.9 = 0.342 м2
h – высота сечения в плоскости действия изгибающего момента;
h=0.38м
е0 – эксцентриситет расчетной силы N относительно центра тяжести сечения;
е0 = M/N = 0.048/44.6 = 0.001м
φ – коэффициент продольного изгиба для всего сечения в плоскости действия изгибающего момента, определяемый по расчетной высоте элемента l0 (см. 7.2, 7.3), по таблице 19;
Таблица 19 [1]

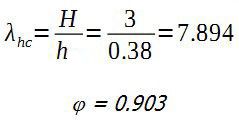
φс – коэффициент продольного изгиба для сжатой части сечения, определяемый по фактической высоте элемента Н по таблице 18 в плоскости действия изгибающего момента при отношении
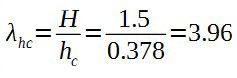
Для прямоугольного сечения hc = h – 2e0 = 0.38 – 2*0.001 = 0.378 м
φс = 1
При знакопеременной эпюре изгибающего момента по высоте элемента (рисунок 12) расчет по прочности следует производить в сечениях с максимальными изгибающими моментами различных знаков. Коэффициент продольного изгиба φс следует определять по высоте части элемента в пределах однозначной эпюры изгибающего момента при отношениях
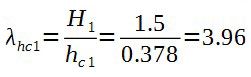
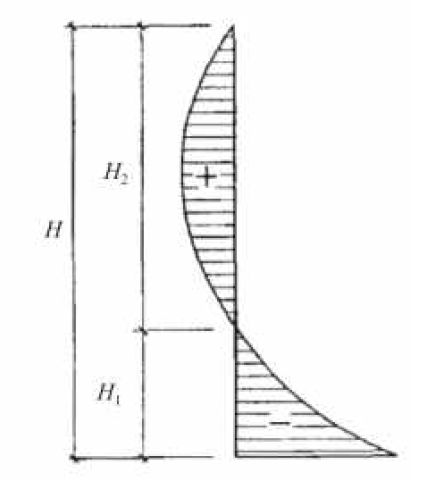
Рисунок 12. Знакопеременная эпюра изгибающего момента для внецентренно сжатого элемента
где Н1 и Н2 – высоты частей элемента с однозначной эпюрой изгибающего момента; hс1; iс1 и hс2; iс2 – высоты и радиусы инерции сжатой части элементов в сечениях с максимальными изгибающими моментами; ω – коэффициент, определяемый по формулам, приведенным в таблице 20;
При h ⩾ 30 см или i ⩾ 8,7 см коэффициент mg следует принимать равным единице.
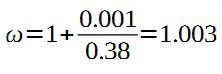
Таблица 20 [1]

Необходимо отметить, что согласно п.п.7.8 [1] при е0 > 0,7у, кроме расчета внецентренно сжатых элементов по формуле (13), следует производить расчет по раскрытию трещин в швах кладки согласно указаниям п.п. 8.3. При действии изгибающего элемента в плоскости простенка дополнительно необходимо выполнить проверку на косое внецентренное сжатие согласно п.п. 7.12.
С учетом вышеобозначенных требований выполним проверку рассматриваемого простенка как находящегося в состоянии внецентренного сжатия:
N=44.6т⩽mgφ1RAcω=1*0.09515*275.3*0.342*1.003=89.85т
- условие выполнено, несущая способность простенка обеспечена, коэффициент использования:
К=44.6 / 89.85 = 0.496
В данной заметке не рассматривается проверка кладки на срез, но согласно требованиям п.п.7.2 [2] расчет неармированной кладки на срез по горизонтальным неперевязанным швам и перевязанным швам кладки следует производить по формуле:
Q⩽(Rsq+0.8nμσ0)A,23
где Rsq – расчетное сопротивление срезу (см. таблицу 11);
μ – коэффициент трения по шву кладки, принимаемый для кладки из кирпича и камней правильной формы равным 0,7; σ0 – среднее напряжение сжатия при наименьшей расчетной нагрузке, определяемой с коэффициентом надежности по нагрузке 0,9; п – коэффициент, принимаемый равным 1,0 для кладки из полнотелого кирпича и камней и равным 0,5 для кладки из пустотелого кирпича и камней с вертикальными пустотами, а также для кладки из рваного бутового камня; А – расчетная площадь сечения.
Проверки на срез и растяжение можно выполнить путем анализа касательных/растягивающих напряжений в пластинах. На участках, в которых напряжения превышают расчетные сопротивления на срез/растяжения необходимо проводить дополнительный анализ, производить физически-нелинейный расчет, анализировать деформации и определять возможность устройства компенсирующих мероприятий.

Рисунок 13. Мозаики касательных напряжений
Расчет стен на вертикальную нагрузку по раскрытию трещин
Следующим этапом проверки кладки является проверка по раскрытию трещин. При различии наружных и примыкающих к ним внутренних стен по степени загрузки или выполнении их из различных материалов участки стен, близкие к местам их взаимного примыкания, [1] рекомендует выполнить расчет по образованию и раскрытию трещин согласно приложению Е. При данном расчете условно принимается, что обе стены (или смежные участки одной и той же стены) не связаны друг с другом, и определяется свободная деформация каждой из двух стен отдельно при действии расчетных длительных нагрузок. Разность свободных деформаций этих стен должна удовлетворять условию
δ1-δ2⩽δu
где δ1 – абсолютная свободная деформация сжатия одной из стен (или участка стены);
δ2 – то же, второй стены;
δu – предельная допустимая разность деформаций, определяемая по таблице Е.1.
Таблица Е.1 [1]

Для того, чтобы выполнить данную проверку изменим расчетную схему с учетом предпосылок, озвученных выше, исключим узлы из согласования сетей, которые находятся на пересечении стен. Для того, чтобы система не стала ГИС, выполняем закрепление освобожденных стен по осям X, Y.
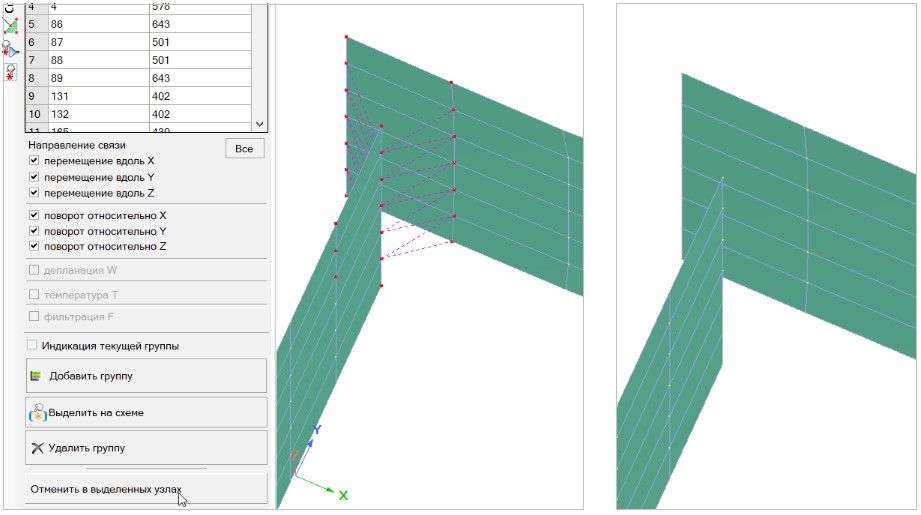
Рисунок 14. Согласование сетей. Исключение узлов из согласования
Выполняем статический расчет на длительные нагрузки и производим анализ. На рисунке 15 отображена мозаика вертикальных перемещений узлов в стенах.

Рисунок 15. Деформированная схема. Мозаика вертикальных перемещений.
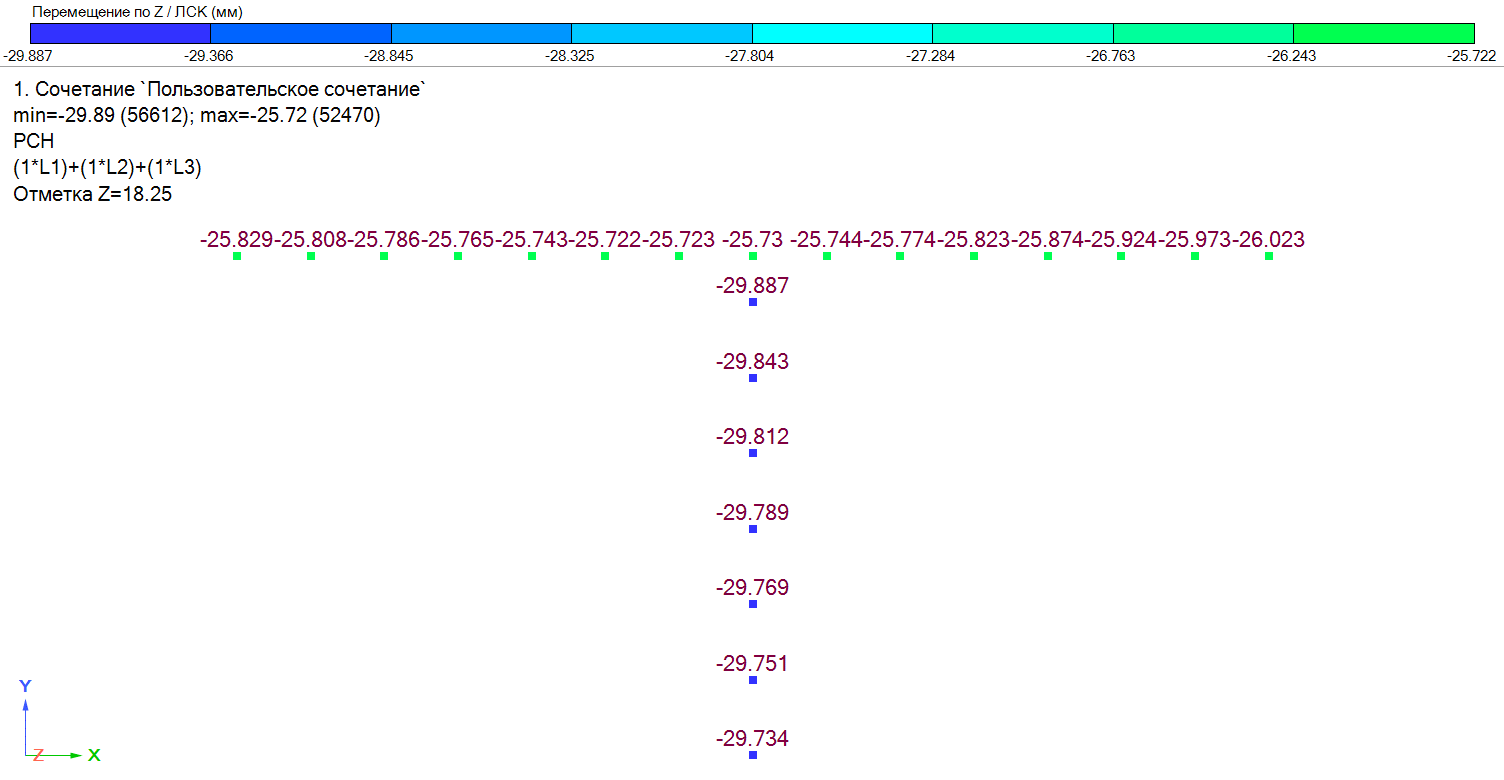
Рисунок 16. Деформированная схема. Мозаика вертикальных перемещений узлов.
На примере одного из пересечений (рисунок 16) выполняем проверку условия разности деформаций по таблице Е.1 [1].
29.89мм - 25.72мм = 4.17мм ⩽ δu = 8мм
- условие выполнено, принятая конструктивная схема удовлетворяет требованиям совместности деформаций.
Автоматизация поверочного расчета кладки на внецентренное сжатие:
Как вы могли заметить, что проверка кладки, как внецентренно-сжатого элемента, в общем случае требует значительного количества вычислений и при большом количестве расчетных простенков, а также при наличии нескольких комбинаций РСН, данный расчет может занять много времени. Для ускорения подобных проверок в ЛИРА 10.12 возможно использовать скрипты написанные на языке программирования C# и загруженные в процессор пользовательских результатов.
Для активации панели данного режима воспользуйтесь командой Спец. результаты ⇨ Пользовательские результаты (кнопка  на панели инструментов).
на панели инструментов).
Рисунок 17. Вкладка Пользовательские результаты
На вкладке Пользовательские результаты выполняется задание и редактирование скриптов. В верхней части панели (рисунок 17) расположен список с уже созданными скриптами. В нижней части — кнопки:
Добавить скрипт — вызывает диалоговое окно для создания нового скрипта.
Изменить скрипт — вызывает диалоговое окно для редактирования существующего скрипта (выбранного в списке).
Удалить скрипт — позволяет удалить из списка ненужный скрипт.
Отобразить — позволяет визуализировать на схеме мозаику, соответствующую выбранному в списке скрипту.
Диалоговое окно для создания / редактирования скрипта (рисунок 18) содержит:
Имя — поле для ввода имени скрипта.
Объекты, по которым будет построена мозаика (Узлы, Стержни, Пластины, Объемные или Спец. элементы).
Настройки единиц измерения, которые будут использоваться при вычислениях.
Метод вычисления — поле для ввода скрипта с использованием синтаксиса языка программирования C#.
Доступные методы — список доступных методов для получения данных из начальных параметров и результатов расчета ПК ЛИРА 10.
Стандартные методы — список доступных дополнительно возможных функций, кроме стандартных функций С#.
При двойном щелчке мыши по строке с нужным методом, его наименование впишется в поле для ввода скрипта, в месте расположения курсора.
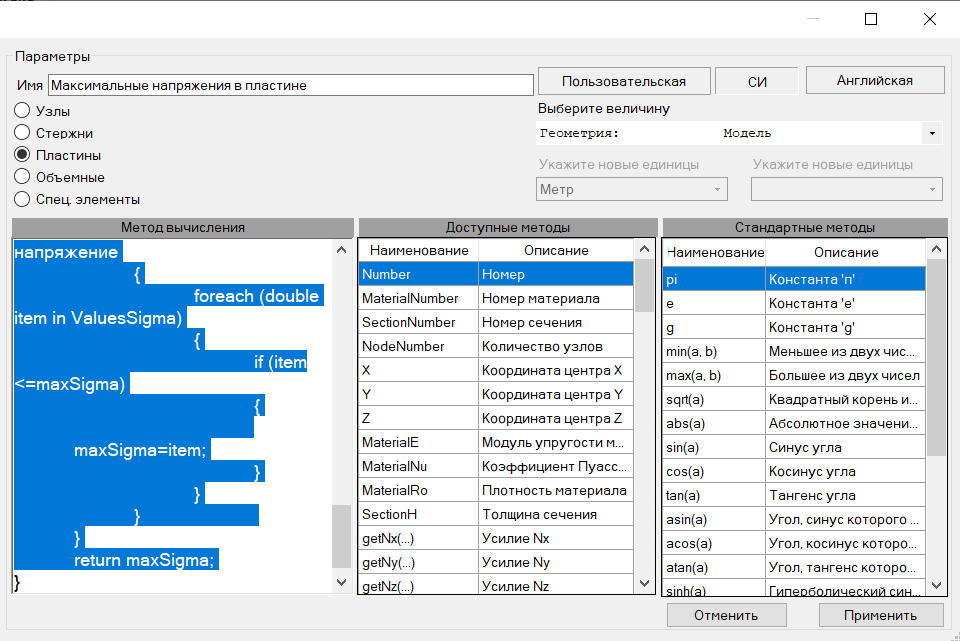
Рисунок 18. Окно для создания / редактирования скрипта
Файл со всеми созданными пользователем скриптами ScaleUserData.xml хранится в папке с файлами шаблонов (рисунок 19), и может быть перемещен, удален или заменен.
Путь: Сервис ⇨ Настройки среды ⇨ Расположение ⇨ Каталог файлов шаблонов ⇨ Templates ⇨ ScaleUserData.xml.
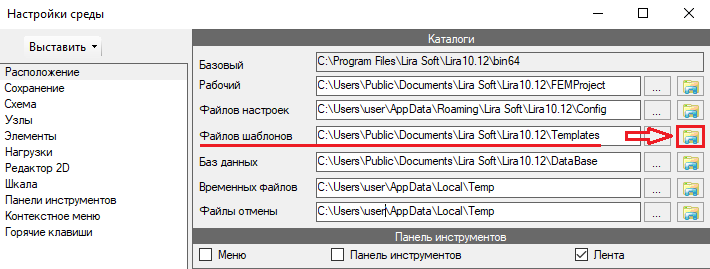
Рисунок 19. Окно для создания / редактирования скрипта
Методы (процедуры и функции) в скрипте:
Скрипт может содержать отдельные методы (процедуры и функции), которые будут использованы в других методах или главном блоке. Если используются вновь созданные методы, то главный блок необходимо взять в фигурные скобки вместе со строкой, имеющей ключевое слово return. Сами методы описываются ниже основного блока, отделенного фигурными скобками.
При объявлении методов должен быть указан тип возвращаемого значения. Если метод является процедурой (без возвращаемого значения), то нужно указать его тип void. Также в скобках, после имени метода, необходимо указать параметры и их тип, кроме тех случаев, когда у метода нету параметров. Дальше в фигурных скобках идут команды метода.
Структура метода:
Тип_метода Имя_метода (тип_параметра1 имя_параметра1, тип_параметра2 имя_параметра2... тип_параметраn имя_параметраn)
{
Выражение 1;
Выражение 2;
…
Выражение m;
return Результат_метода; (если тип метода void, то return не используется)
}
Использование комментариев в скрипте:
После двух символов // строка не будет участвовать в коде и может быть использована в виде комментария.
Пример:
// Однострочный комментарий
Между /* и */ можно использовать много строк в виде комментариев. Этот инструмент, в том числе, позволяет выключить некоторые строки кода из расчета, не удаляя их насовсем.
Пример закомментированного участка кода:
/*
A=b+c;
return z;
*/
Используя озвученный функционал, составим скрипт для решения нашей практической задачи, для расчета несущей способности кирпичных простенков для заданной комбинации РСН, при составлении дополняем скрипт поясняющими комментариями.
//Основной блок
{
//// Значение задает пользователь ////
double R = 275.3; //расчетное сопротивление кладки на сжатие, т/м.кв.
double H = 3; //расчетная высота простенка, м
//// Значение задает пользователь ////
double[] Loads = {getNRsn (1,0,0),getMzRsn (1,0,0)}; //получение усилий для РСН №1, т
double B = Geom(SectionNumber)[0]; //получаем толщину простенка, м
double L = Geom(SectionNumber)[1]; //получаем ширину простенка, м
double safetyFactor = SafetyFactor(Loads, B, L, H, R); //определяем коэф. использования
return safetyFactor; //вывод значения на мозаику
}
public double SafetyFactor(double[] load, double B, double L, double H, double R) //функция проверки кладки
{
//double[] load {N, My} - усилия
double A = B * L;
if (A < 0.31)
{R=R*0.8;}
double mg = 1; // расчет кладки толщиной более 30см
double e0 = Math.Abs(load[1] / load[0]); //эксцентриситет по Y
double hc = B - 2 * e0; //высота сжатой зоны по Y
double Yhc = H / hc/2; //гибкость сжатой части
double Yh = H / B; //гибкость всего сечения
double Ac = A * (1 - 2 * e0 / B); //площадь сжатой части сечения
double fi1 = (Fi(Yhc) + Fi(Yh)) / 2;
double omega = Omega(e0, B);
double safetyFactor = load[0] / (mg * fi1 * R * Ac * omega); //ф. 7.4 СП 15
if (e0>0.7*hc/2) //проверка п.п.7.8
{
safetyFactor = 999;
}
return safetyFactor; //возвращение коэффициента использования
}
public double Fi(double Y) //функция для вычисления fi при alpha 750 (т. 7.1 СП 15)
{
double fi = 1;
double[,] tableFi = { { 0, 750 }, { 4, 1.00 }, { 6, 0.95 }, { 8, 0.90 }, { 10, 0.84 }, { 12, 0.79 }, { 14, 0.73 }, { 16, 0.68 }, { 18, 0.63 }, { 22, 0.53 }, { 26, 0.45 }, { 30, 0.39 }, { 34, 0.32 }, { 38, 0.26 }, { 42, 0.21 }, { 46, 0.16 }, { 50, 0.13 }, { 54, 0.10 } }; //таблица 7.1 СП 15
if (Y < 4) { fi = 1; }
if (Y > 54) { fi = 0.1; }
if (Y >= 4 && Y <= 54)
{
for (int i = 1; i < (tableFi.Length/2 - 1); i++)
{
if (Y >= tableFi[i, 0] && Y <= tableFi[i + 1, 0]) //поиск ячейки
{
double delta = (Y - tableFi[i, 0]) / (tableFi[i + 1, 0] - tableFi[i, 0]);
fi = tableFi[i, 1] - (tableFi[i, 1] - tableFi[i + 1, 1]) * delta;
}
}
}
return fi;
}
public double Omega(double e0, double h) //т.20.
{
double omega = 1 + e0 / h;
if (omega>1.45)
{
omega = 1.45;
}
return omega;
}
public double[] Geom(int NumSection) //чтение информации о сечении
{
string pathLog = @"C:\Users\Public\Documents\Lira Soft\Lira10.12\FEMProject\Brick\Сечения.csv"; //путь к файлу (задает пользователь)
string[] arrLine = System.IO.File.ReadAllLines(pathLog, System.Text.Encoding.GetEncoding("windows-1251")); //чтение файла сечений
double[] Geom = {0,0};
for (int i = 1; i < arrLine.Length; i++)
{
string[] strs; //массив для хранения строки
strs = arrLine[i].Split(new char[] { ';' }); //запись строки в массив
if (Convert.ToInt32(strs[0]) == NumSection)
{
string[] section = strs[5].Split(new char[] { ',' });
//Geom[0] = Convert.ToDouble(section[0].Replace('.', ',')); //B
//Geom[1] = Convert.ToDouble(section[1].Replace('.', ',')); //H
Geom[0] = Convert.ToDouble(section[0]); //H
Geom[1] = Convert.ToDouble(section[1]); //L
}
}
return Geom;
}
Добавляем данный скрипт в окно метода вычисления и нажимаем применить.
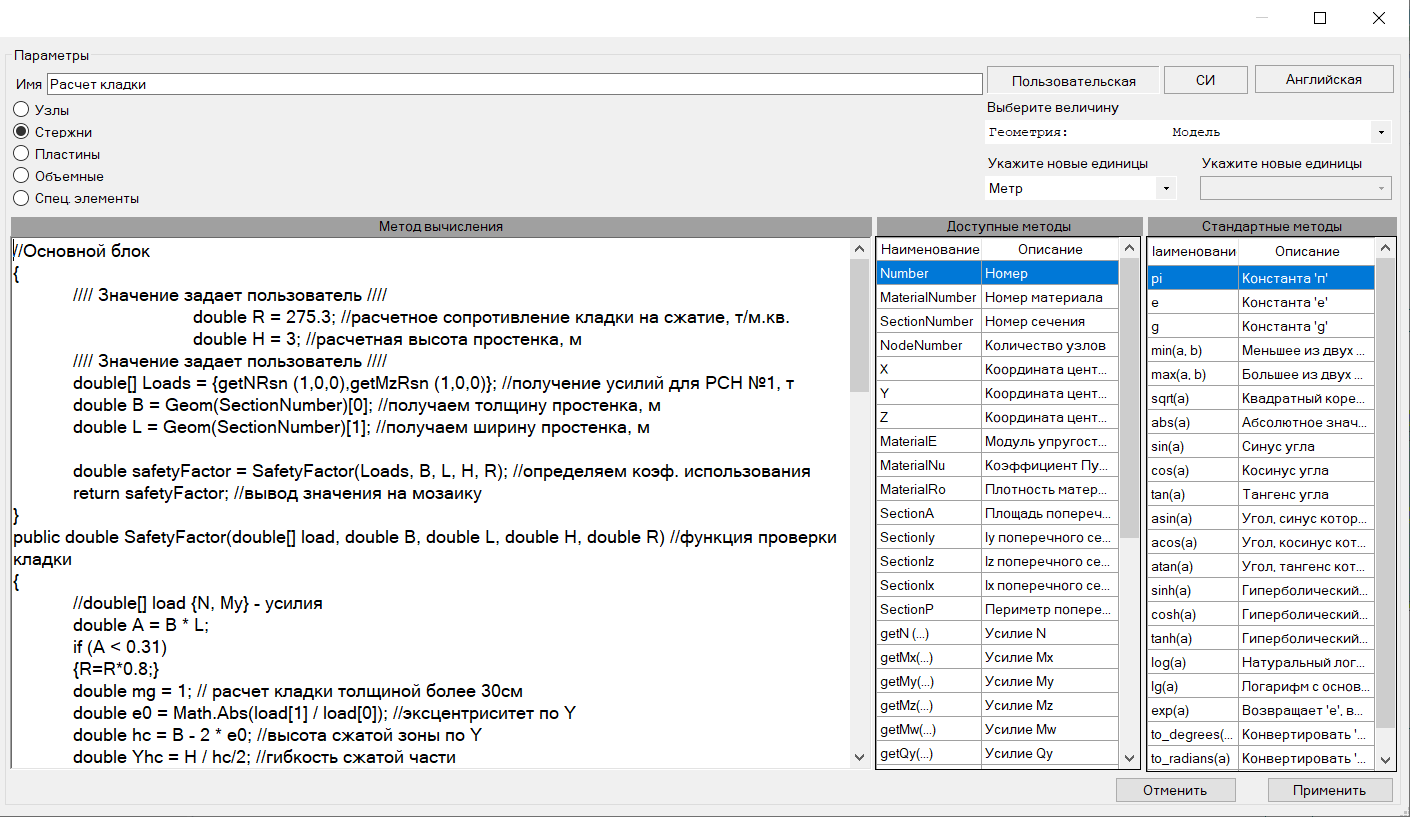
Рисунок 20. Окно для создания / редактирования скрипта
Далее запускаем скрипт нажатием на кнопку отобразить, если скрипт сработает корректно, то в элементах отобразится результат проверки в виде процента использования сечения.
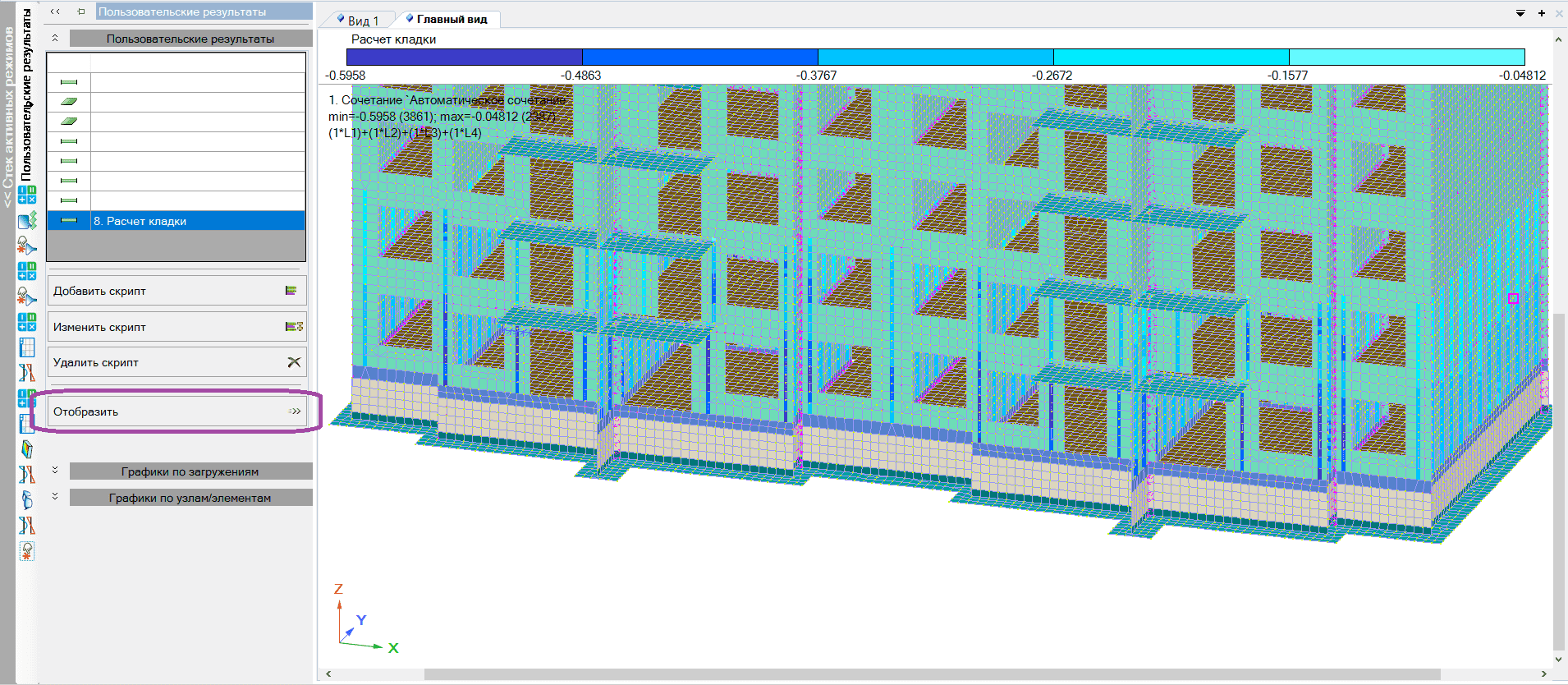
Рисунок 21. Вкладка Пользовательские результаты. Запуск скрипта, просмотр результатов.
Выполним верификацию расчета путем сравнения результата с ранее произведенным ручным расчетом, результат расчета для рассматриваемого простенка отображен на рисунке 22.
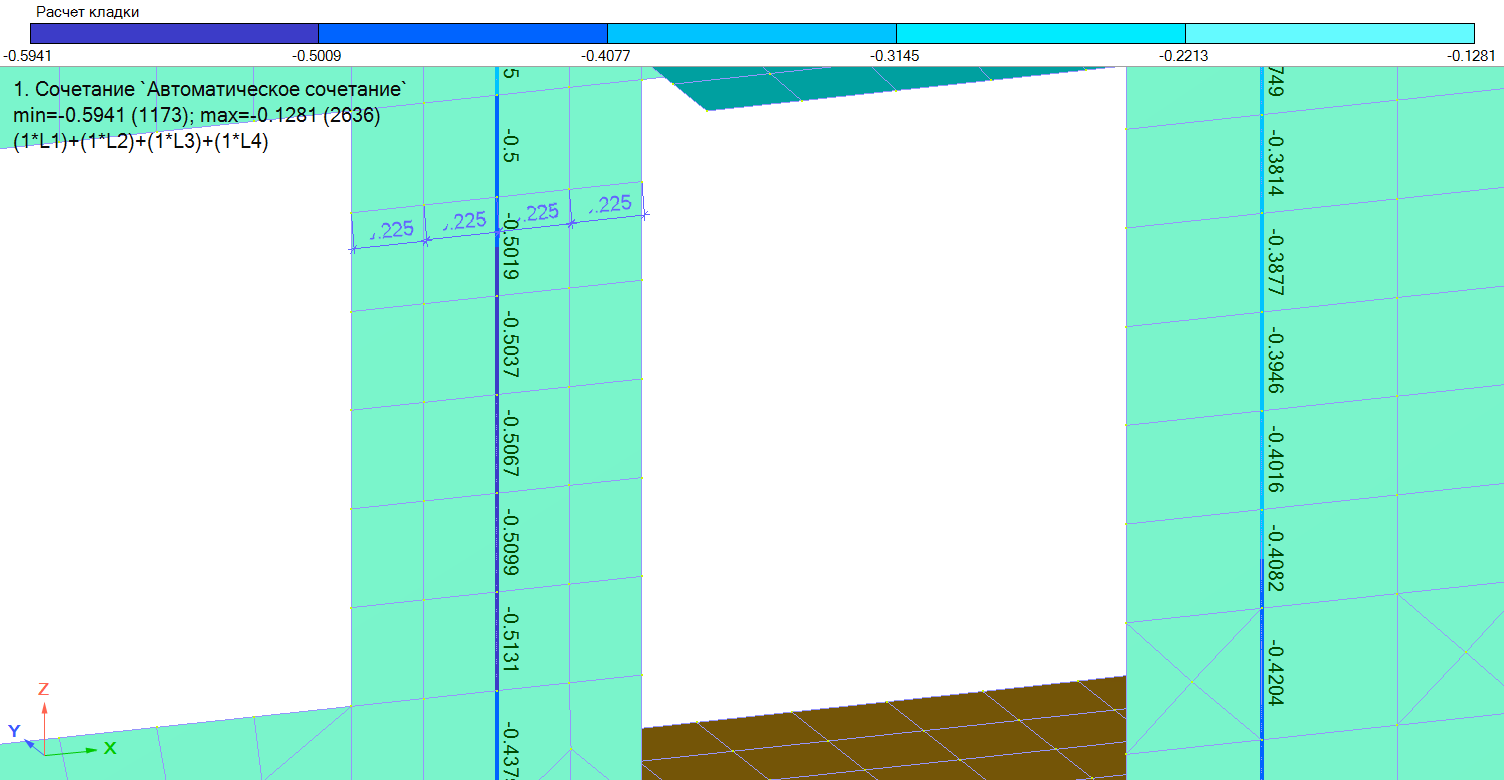
Рисунок 22. Мозаика процента использования сечения простенка, результат работы пользовательского скрипта.
Сравнивая результат, вычисленный ранее вручную – 0.496 и полученный в процессе работы скрипта – 0.501, делаем вывод, что результаты верные и допустимо оценить расчеты в смежных простенках.
Далее при составлении своих собственных скриптов рекомендуем вам обязательно производить верификацию, решать тестовые задачи, анализировать их результаты и только после этого использовать скрипт для рабочих задач, так как при написании скрипта есть вероятность пропустить ряд исключений или особых комбинаций, которые в дальнейшем могут дать ошибку.
В данной заметке мы с вами рассмотрели возможности применения ПК ЛИРА 10 для расчета кирпичных зданий, а также оценили возможности скриптов пользовательских результатов, увидели, как пользователь может самостоятельно решить специфические задачи, которые впрямую не реализованы в программе, выполнить проверки, проверить объемы материалов и т.д. В следующих наших материалах мы будем продолжать демонстрировать возможности пользовательских скриптов, следите за нашими анонсами. Материал не имеет цели охватить все тонкости расчета кирпичных зданий, таких как, нелинейная работа, трещинообразование и т.д., а является иллюстрацией того, как можно выполнить расчет кирпичного здания с учетом определенных предпосылок и допущений.