Содержание:
- Постановка задачи
- Способы моделирования балки в составе монолитного перекрытия
- Определение усилий и перемещений балки МКЭ в линейной постановке
- Проверка сечений балки по результатам линейного расчета
- Определение усилий и перемещений балки МКЭ в НЕлинейной постановке
- Проверка сечений балки по результатам НЕлинейного расчета
- Выводы
Постановка задачи
Проблема расчета монолитных железобетонных балок в составе железобетонного перекрытия методом конечных элементов заключается в получении достоверных результатов расчета для проверки как самой балки, так и примыкающей к ней части перекрытия по 1му и 2му предельному состоянию.
В данной заметке рассмотрен неразрезной пятипролетный участок перекрытия шириной 1 м с балкой, опирающейся на колонны.

Рисунок 1. Продольный вид рассчитываемого участка перекрытия
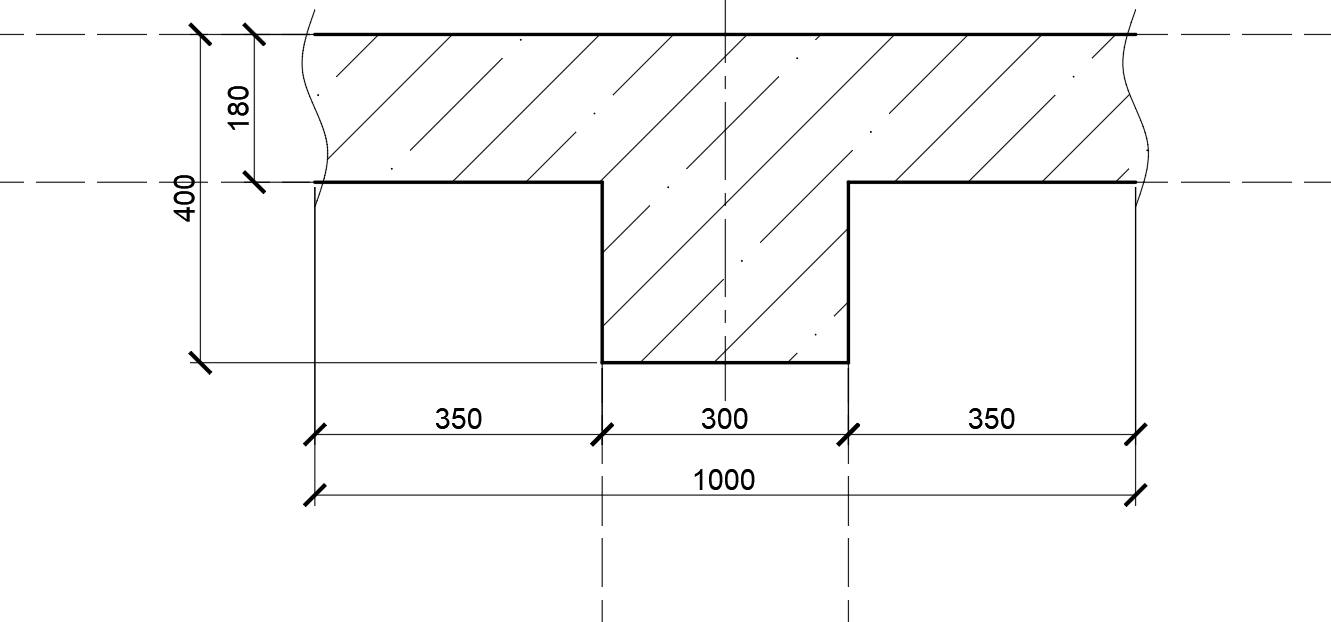
Рисунок 2. Поперечное сечение фрагмента плиты
Цель: найти способ комбинированного моделирования таврового сечения, соответствующего стрежневому аналогу, получить усилия, перемещения и напряжения в элементах балки, процент использования по 1му и 2му предельному состоянию, а также найти наиболее оптимальный способ задания подобной конструкции в реальных задачах.
Способы моделирования балки в составе монолитного перекрытия
Балку в монолитных перекрытиях, как правило, моделируют пластинчатыми горизонтальными а) или вертикальными б) элементами, а также тавровым в) или прямоугольным сечением г). Для учета несносности часто используют жесткие вставки (Рисунок 3). Подробнее о способах моделирования см. https://lira-soft.com/wiki/notes/69-modelirovanie-monolitnykh-plit-po-balkam-v-lira10/
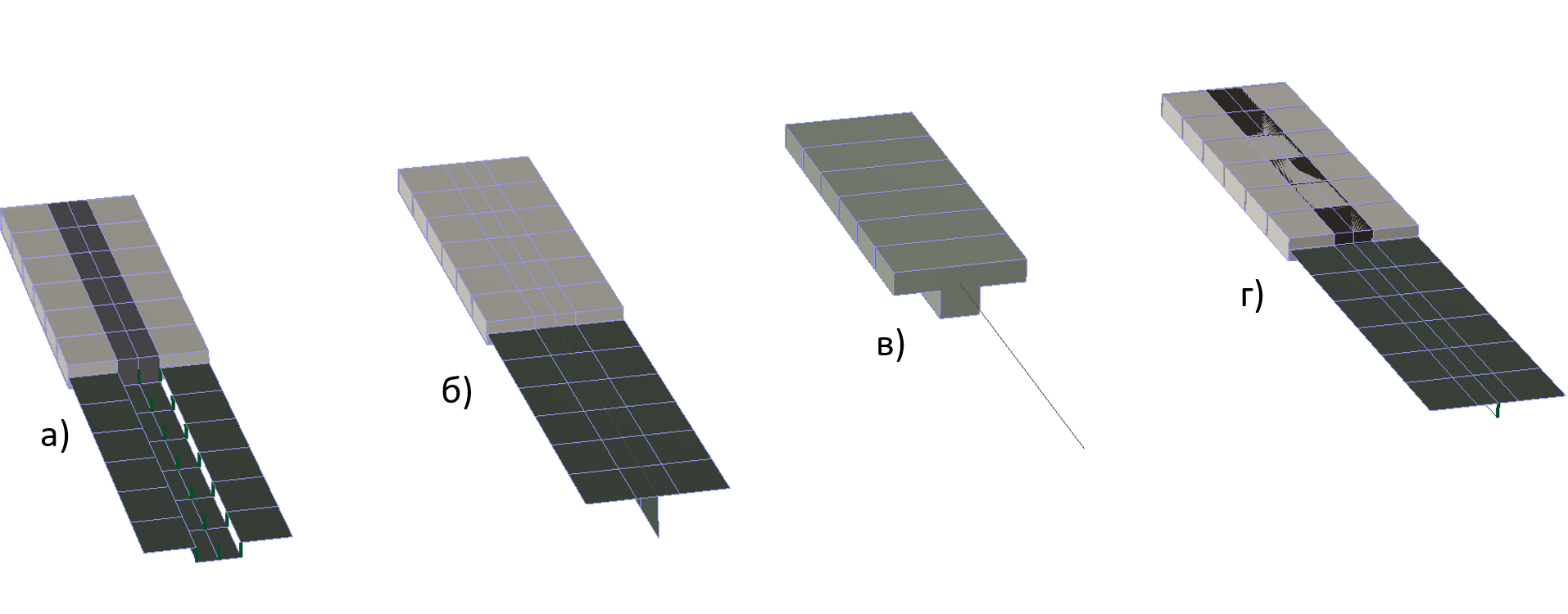
Рисунок 3. Примеры моделирования ребра балки в составе монолитного перекрытия
Моделирование балки в виде стержня в), г) имеет ряд преимуществ:
- в сечении возможно указать точную привязку продольных арматурных стержней относительно двух координат;
- балке из стержневого КЭ легко менять сечение;
- доступна проверка балки по прочности пространственного сечения (СП 63.13330.2018 П 8.1.40);
- возможен учет конструктивных особенности балки при расчете.
При моделировании фрагмента перекрытия в виде пластин и прямоугольного стержня г) в месте их пересечения образуется зона, в которой тело балки входит в сечение плиты. Данная погрешность увеличивает жесткость фрагмента (Рисунок 4).
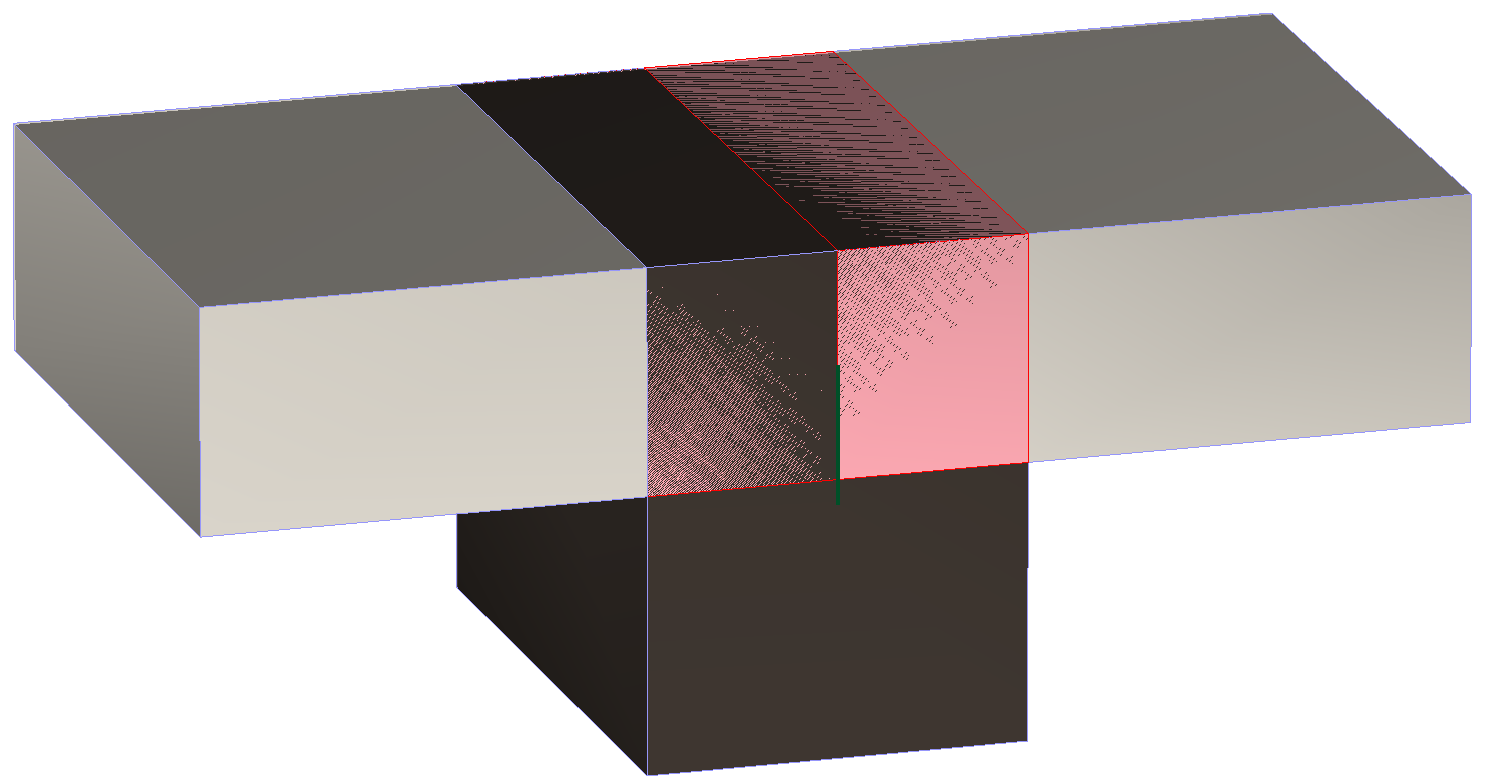
Рисунок 4. Задвоение жесткостей при физическом представлении участка перекрытия
Для её устранения можно уменьшить сечение стержня балки а) или удалить часть пластин б) (Рисунок 5)
Первый способ затрудняет дальнейший расчет арматуры балки. Второй способ более предпочтителен для дальнейшего расчета конструирования, но более трудоемкий, так как требует удаления части пластин на ширину балки. Для соединения узлов элементов можно применить твердые тела.
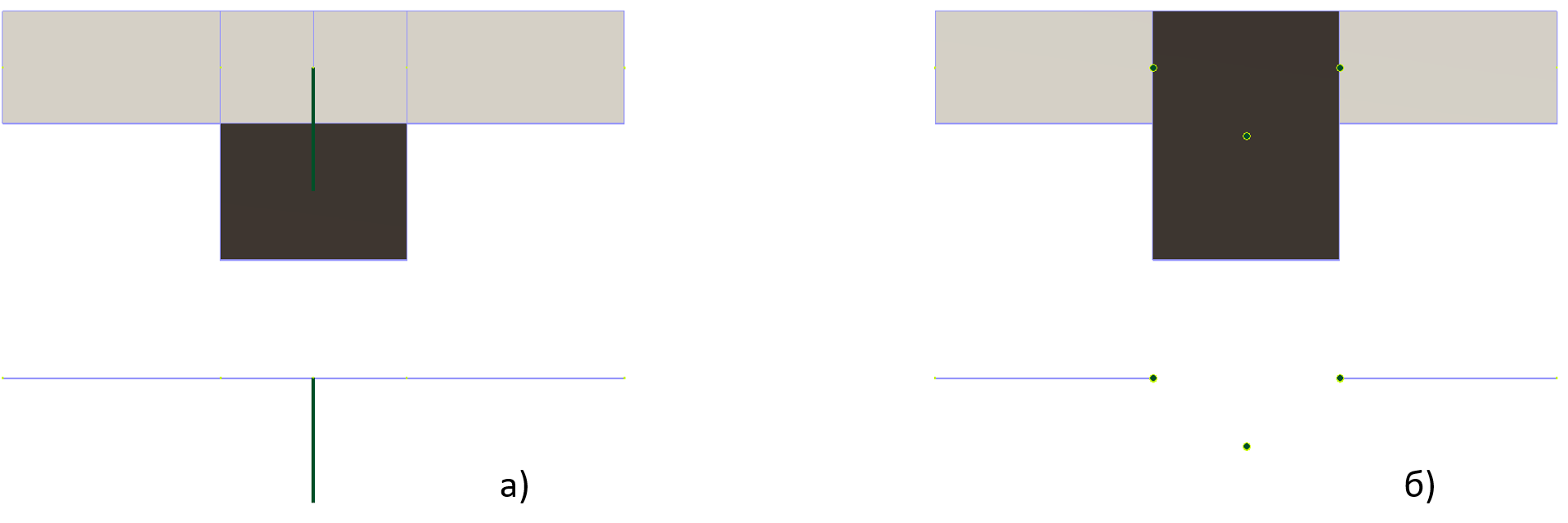
Рисунок 5. Способы моделирования ребра балки без задвоения жесткостей
Определение усилий и перемещений балки МКЭ в линейной постановке
Выполним расчет фрагмента перекрытия (Рисунок 6), представленный:
- единым тавровым стержнем;
- стержнем и пластинами с учетом жесткой вставки и без центральной части балки;
- стержнем и пластинами с учетом жесткой вставки;
- стержнем соосным с пластинами.
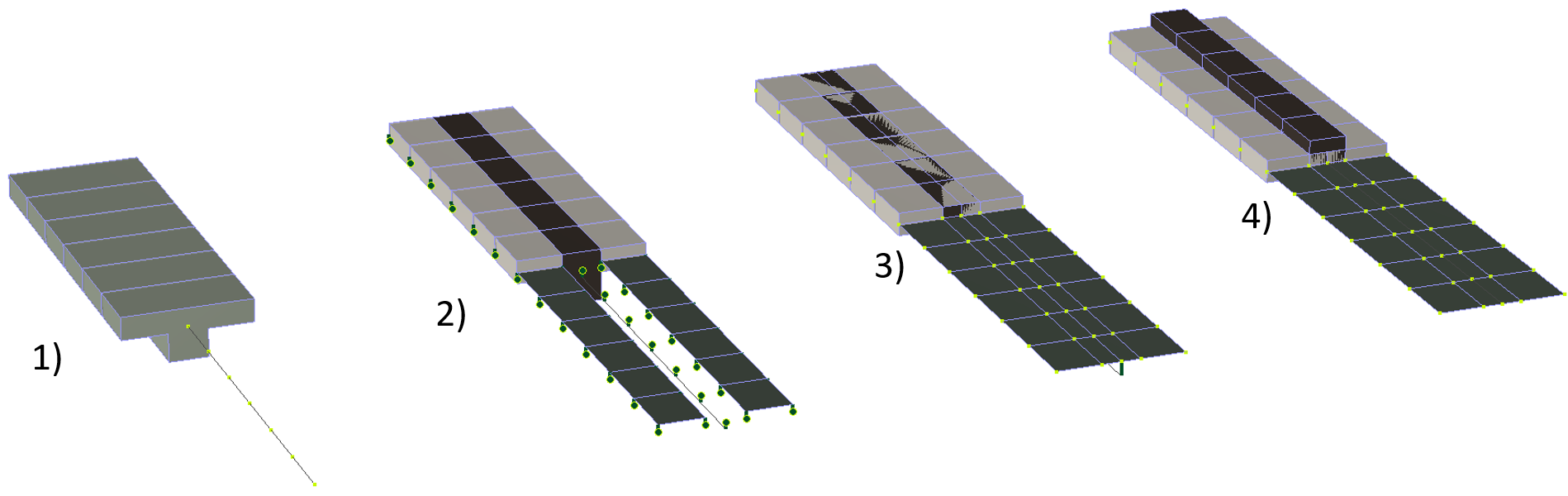
Рисунок 6. Виды фрагмента перекрытий, представленных к сравнению
Исходные данные для основного расчета
Размеры и жесткость:
Шесть колонн, высотой 3 м, сверху на колонны жестко опирается тавровый фрагмент перекрытия пролетом балок 6 м (Рисунок 1).
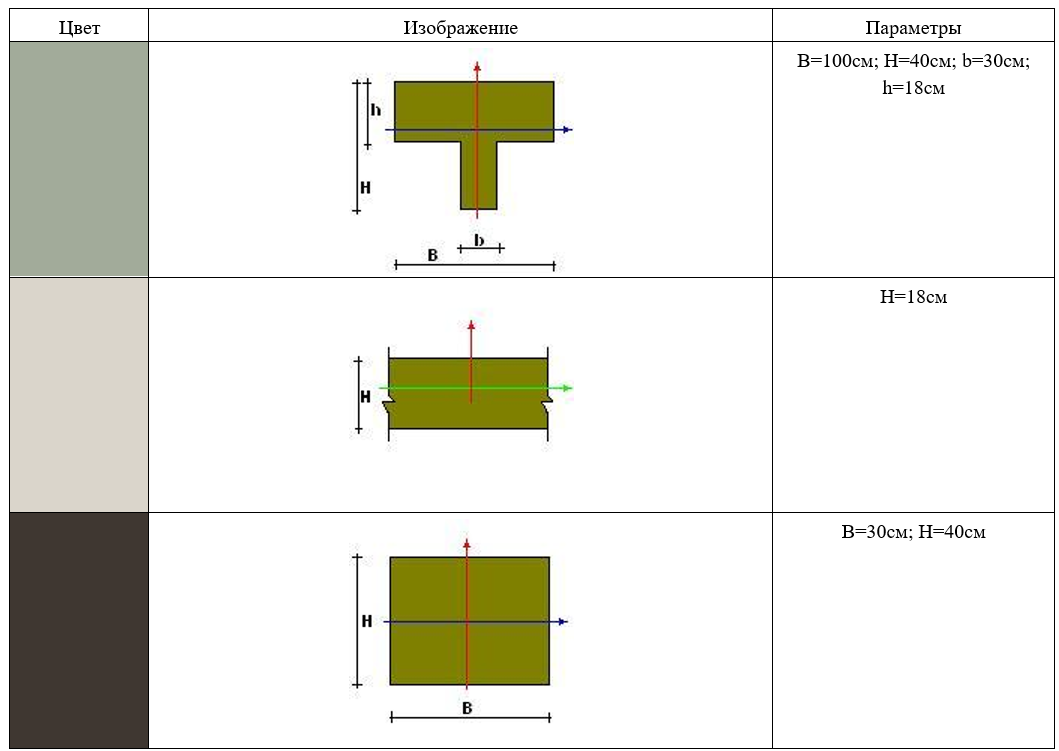
Таблица 1. Параметры заданных сечений
Модуль деформации горизонтальных конструкций 9000 мПа, вертикальных 18000 мПа. Коэффициент Пуассона Nu=0.2
Нагрузки:
Нагрузка на фрагмент равна 6тс/м (Рисунок 7).
В случае 2) часть нагрузки, приложенная на балку равна 6*0,3=1,8 тс, где 0,3 ширина ребра.
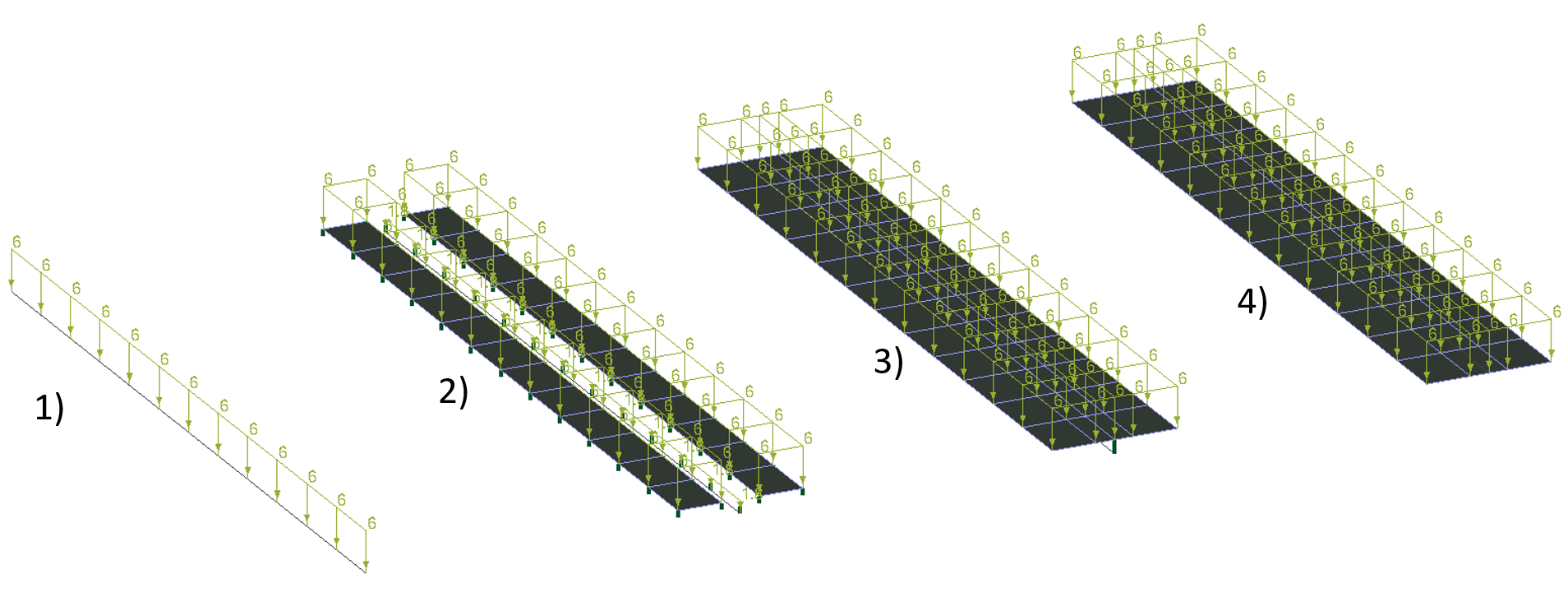
Рисунок 7. Нагрузки приложенные на фрагменты монолитного перекрытия
Граничные условия и соединение элементов
Узлы основания колонн имеют жесткие связи. Все узлы жесткие.
В случае 3) стержню заданы жёсткие вставки на -0.11 м.
В случае 2) задана система жестких вставок и твердых тел, которые лежат на нормалях к балке.
Шаг триангуляции
Фрагмент плиты задан с шагом 0,5 м вдоль пролета.
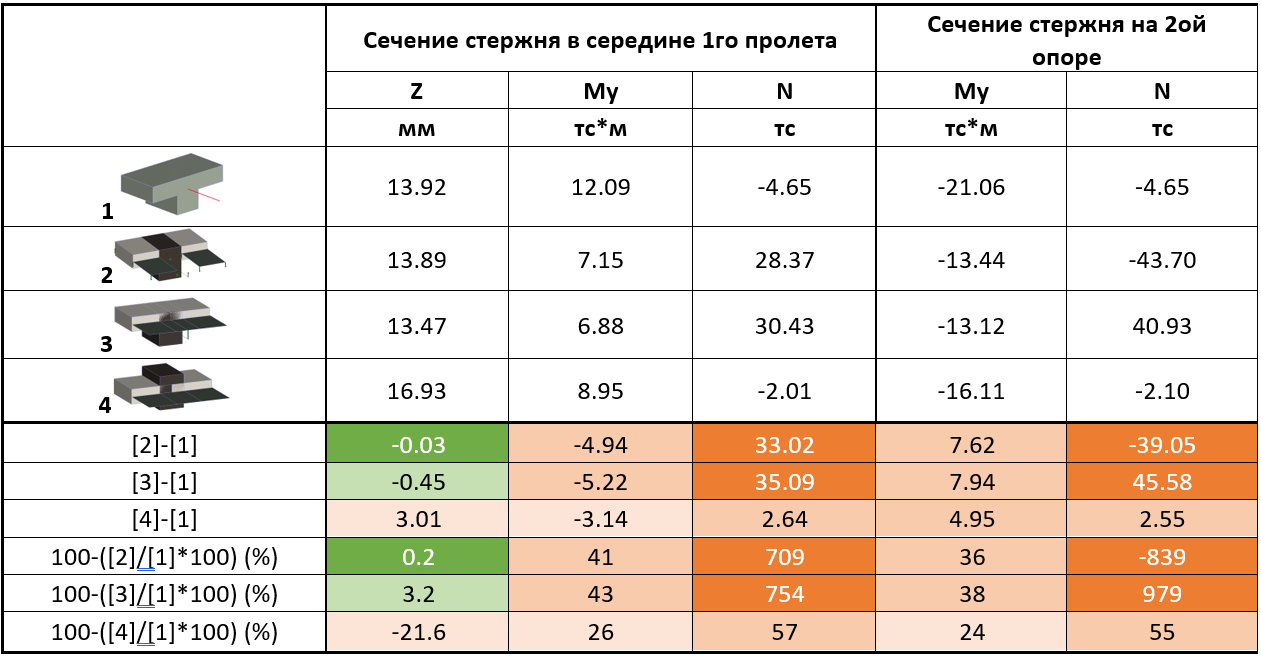
Таблица 2. Результаты линейного расчета
Максимальные перемещения узлов в 1, 2 и 3 схеме имеют схожие значения, 4 схема имеет перемещения выше, так как полученное крестовое сечение фрагмента имеет меньший момент инерции.
Усилия в стержне в 2,3 схемы отличаются от 4 схемы из-за того, что при введении жесткой вставки часть изгибающего момента переходит в продольное усилие, в следствии чего в 2 и 3 схеме продольные силы значительно выше. Результаты 2, 3 и 4 схемы отличаются от 1, тем, что часть усилий воспринимается пластинами.
Проверка сечений балки по результатам линейного расчета
Усилия являются одним из значений необходимым для проверки сечения по 1му и 2му предельному состоянию.
Зададим одинаковое армирование и параметры конструирования для всех 4х схем и сравним процент использования по прочности и трещиностойкости.
- Армирование ребра: 4d20 – верхняя, 2d20 – нижняя
- Армирование перекрытия: d12s200 верхняя и нижняя
Исходные данные для выполнения расчета на конструирование
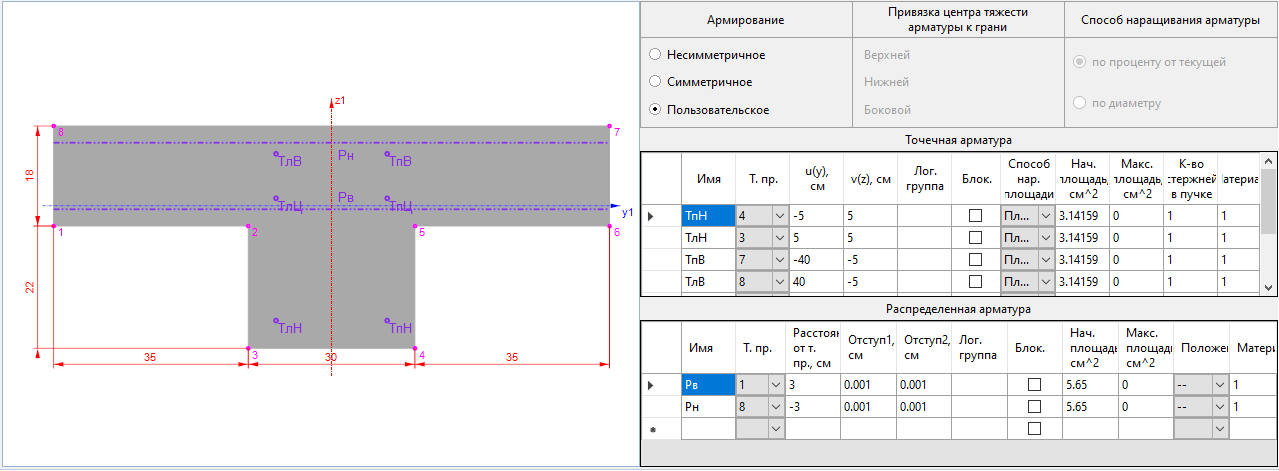
Рисунок 8. Заданное армирование тавра (1 схема)
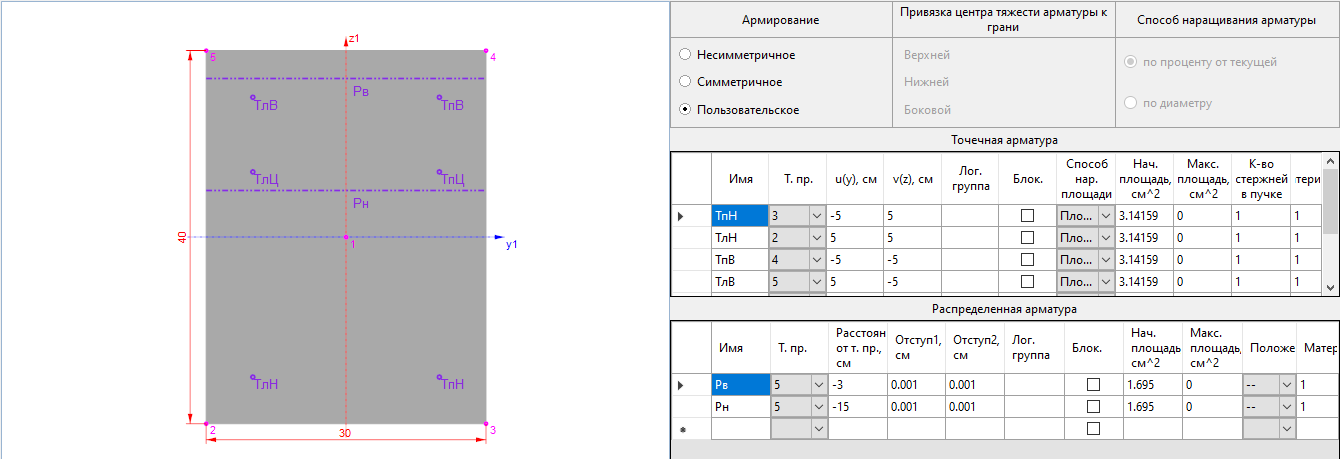
Рисунок 9. Заданное армирование ребра (2 схема)
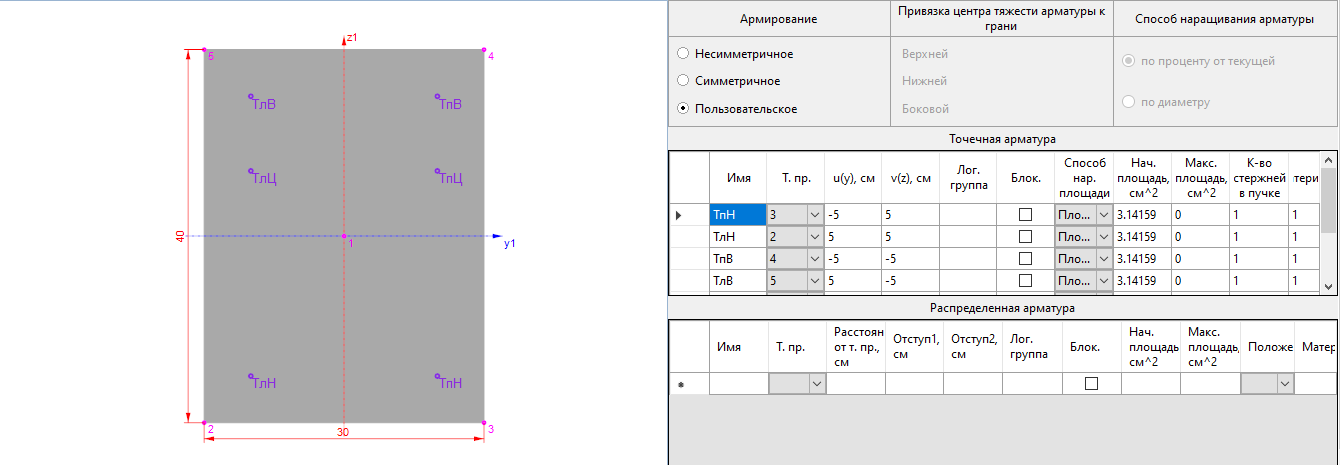
Рисунок 10. Заданное армирование ребра (3, 4 схема)
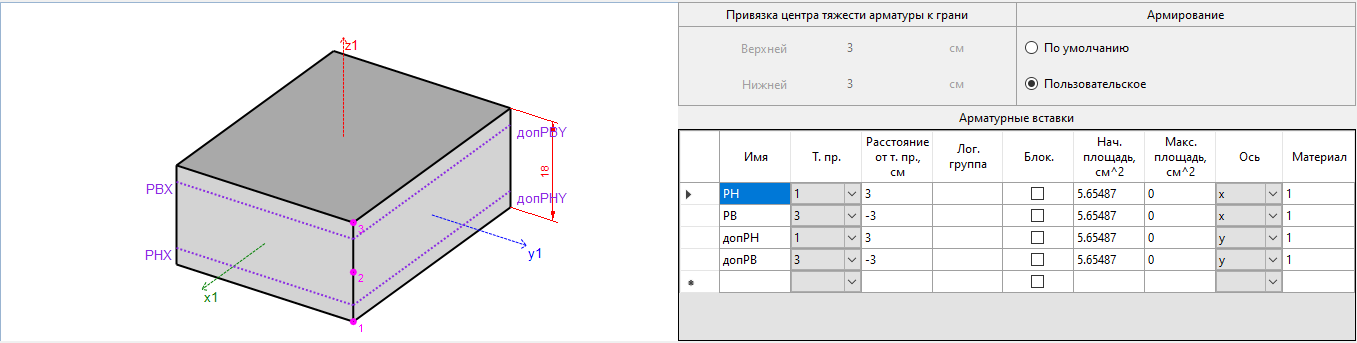
Рисунок 11. Заданное армирование полок тавра (2, 3, 4 схема)
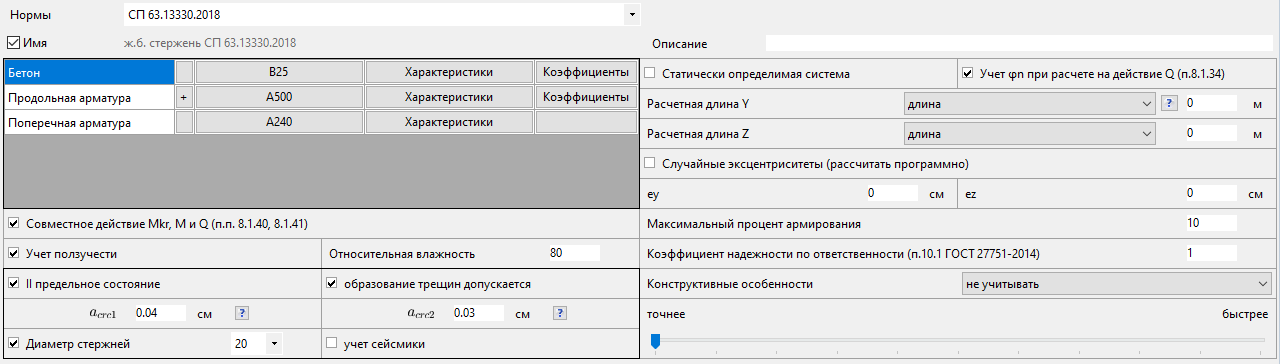
Рисунок 12. Конструирование стержней
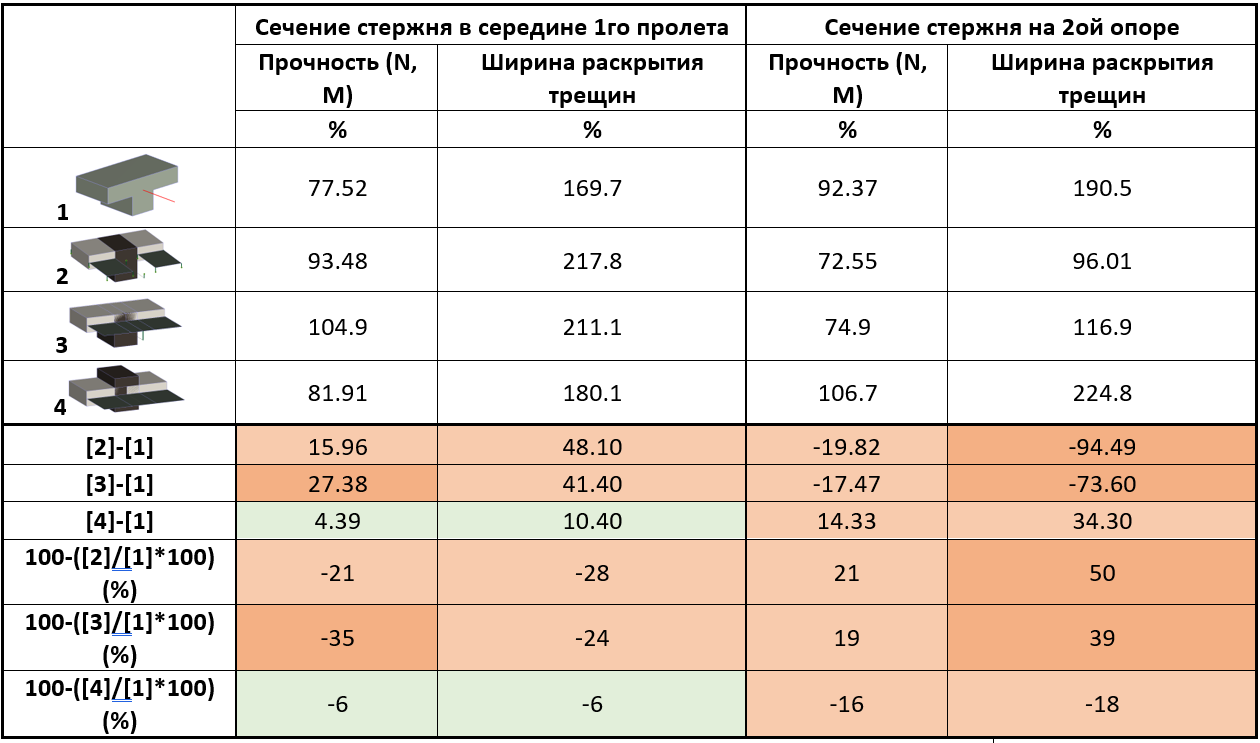
Таблица 3. Результаты проверки сечений от полученных усилий в линейном расчете
Результаты расчета проверки сечений показывают значительную разницу как по прочности, так и по трещиностойкости практически во всех 4х методах. Что не позволяет сделать вывод о применении того или иного способа моделирования подобных конструкций.
Большой разброс данных конструирования основан на неверных исходных данных для расчета.
При сравнении 1го и 2го метода моделирования участка перекрытия стержни показывают схожую картину напряжено-деформированного состояния (Рисунок 13), что подтверждается также анализом напряжений крайних волокон сечения элемента как в пролете, так и на опорах.
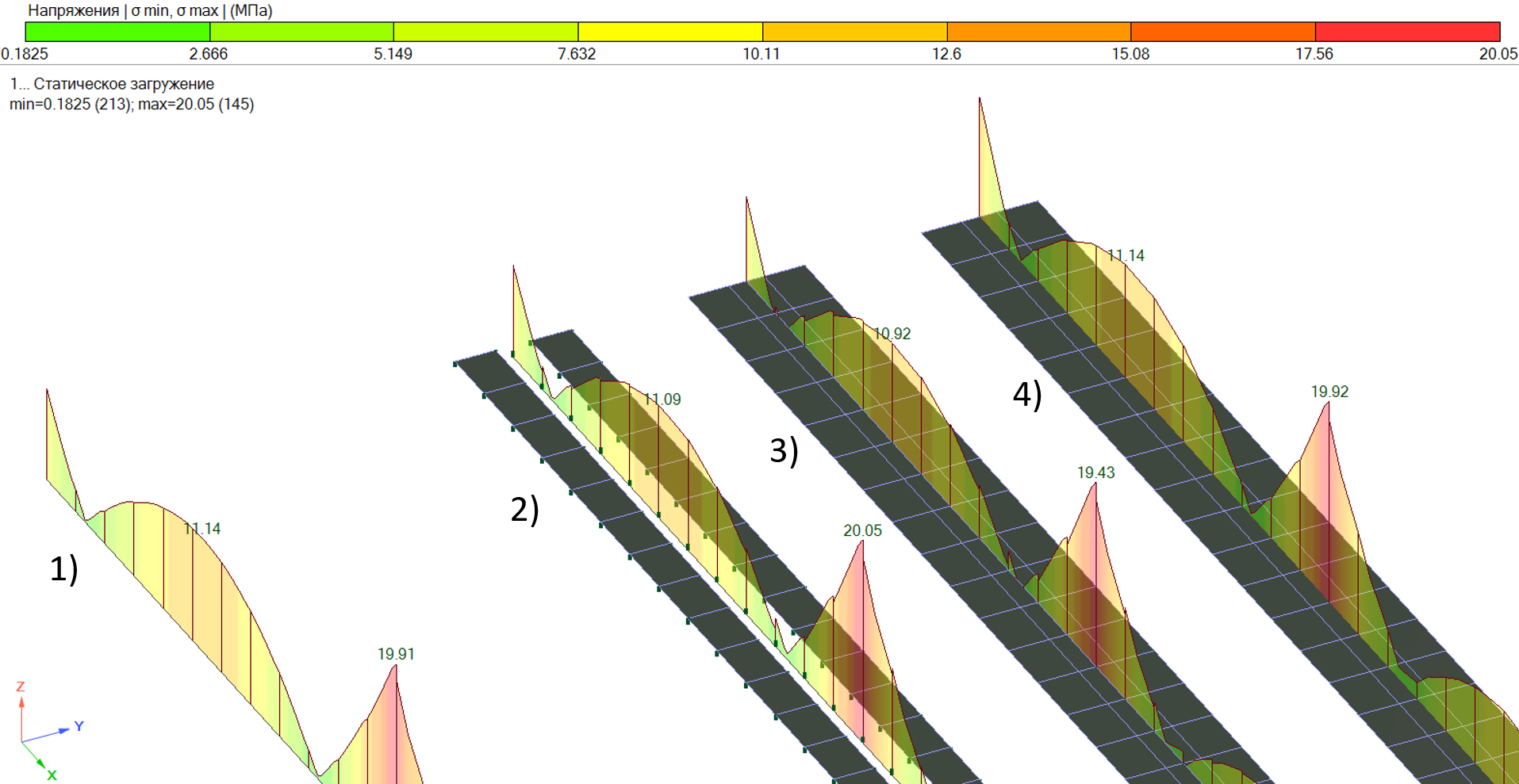
Рисунок 13. Напряжение в сечении стержня
Подобная картина напряжений имеет место быть только для однородных сечений элемента, что характерно для таких материалов как сталь. Железобетон же имеет в составе как бетон, так и сталь, при этом каждый из которых работает по нелинейному закону деформирования. Соответственно и уточнить усилия в элементах можно с помощью нелинейном расчете.
Определение усилий и перемещений балки МКЭ в НЕлинейной постановке
Исходные данные для нелинейного расчета
Тип конечных элементов:
- Горизонтальные стержни: КЭ 210 Физический нелинейный универсальный шаговый КЭ пространственного стержня
- Горизонтальные пластины: КЭ 242,244 Физический нелинейный шаговый КЭ тонкой оболочки
Материал:
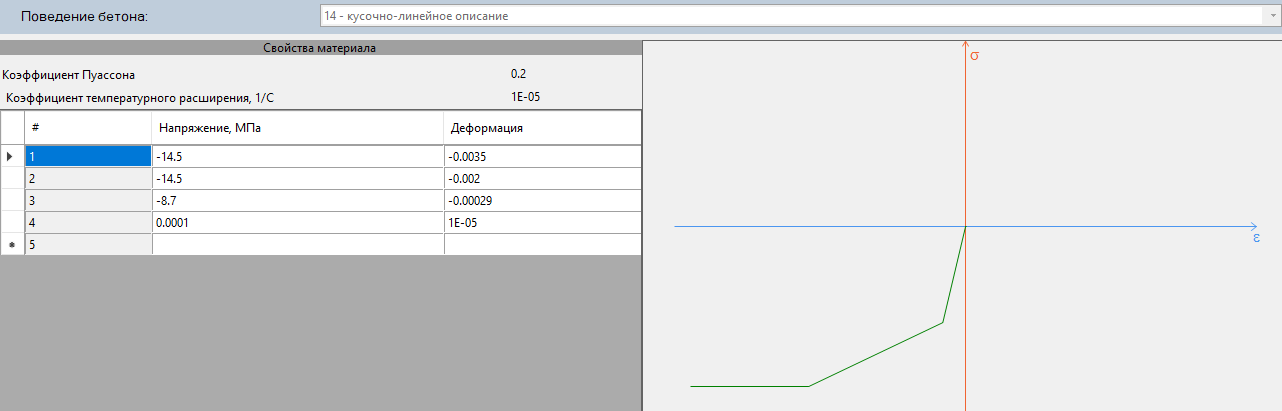
Рисунок 14. График работы бетона
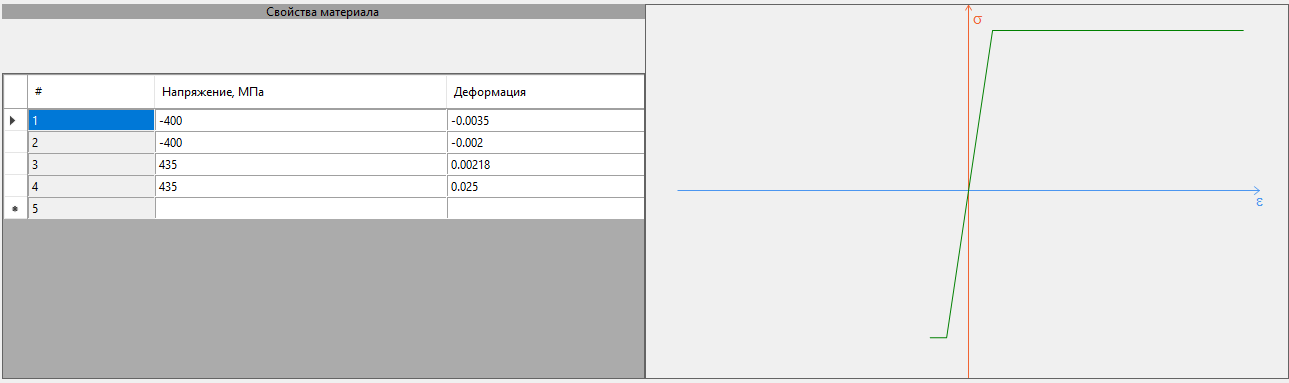
Рисунок 15. График работы арматуры
История нелинейного загружения
- Автоматический выбор шага
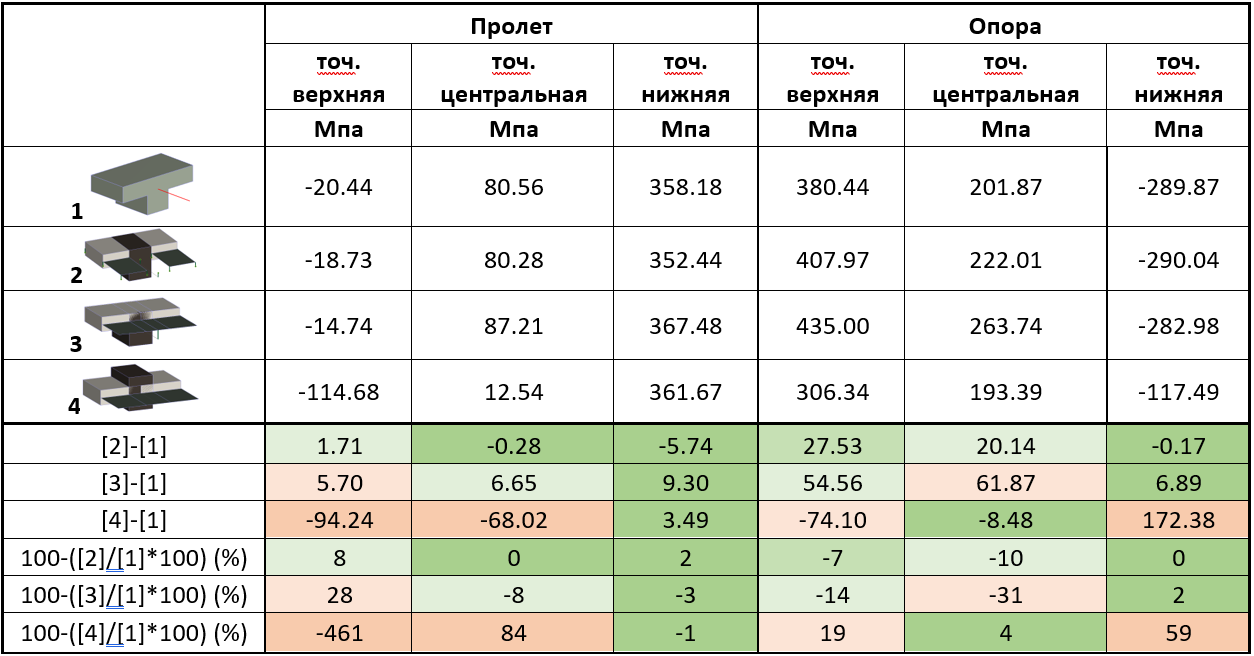
Таблица 4 Результаты нелинейного расчета: напряжения точечной арматуры
По таблице 4 видно, что схемы 1 и 2 близки по работам. Значение из 4 схемы существенно отличается от прочих.
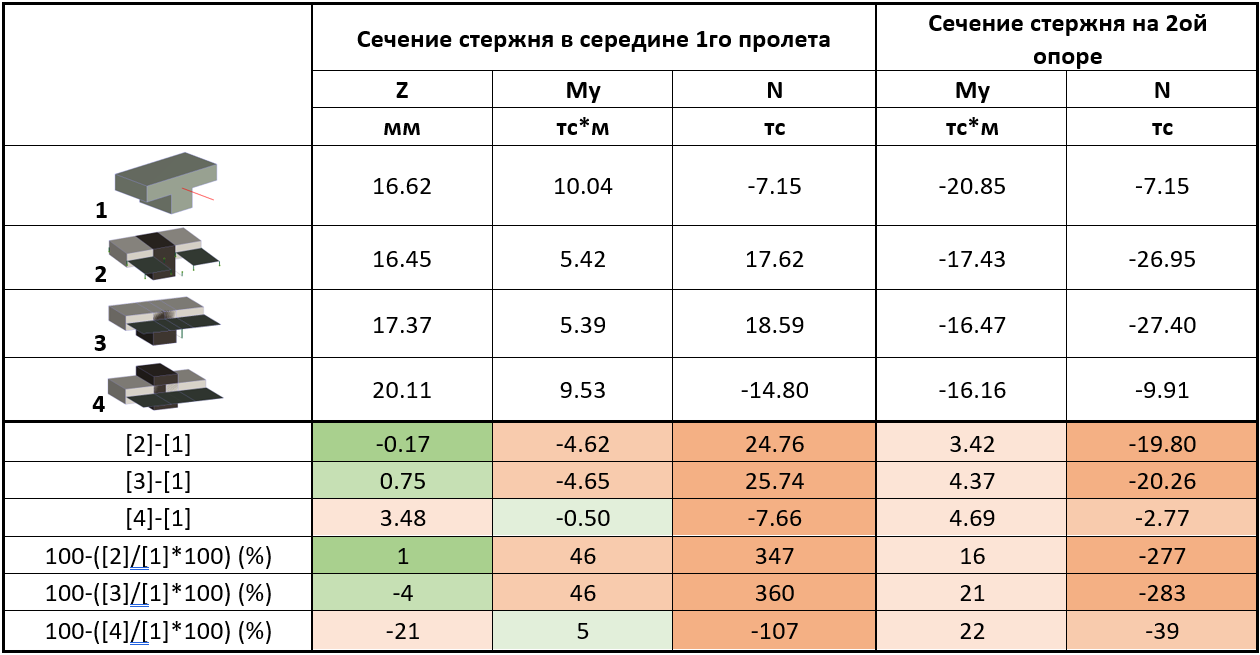
Таблица 5 Результаты нелинейного расчета: усилия в сечении элементов
Как и в линейной задаче погрешность в прогибах балок увеличивается с 2 по 4 схему по отношению к схеме №1. Усилия в схеме отличаются еще больше, чем в линейной задаче.
Проверка сечений балки по результатам НЕлинейного расчета
Зададим полученные усилия сечениям соответствующих элементов для проверки по прочности и трещиностойкости
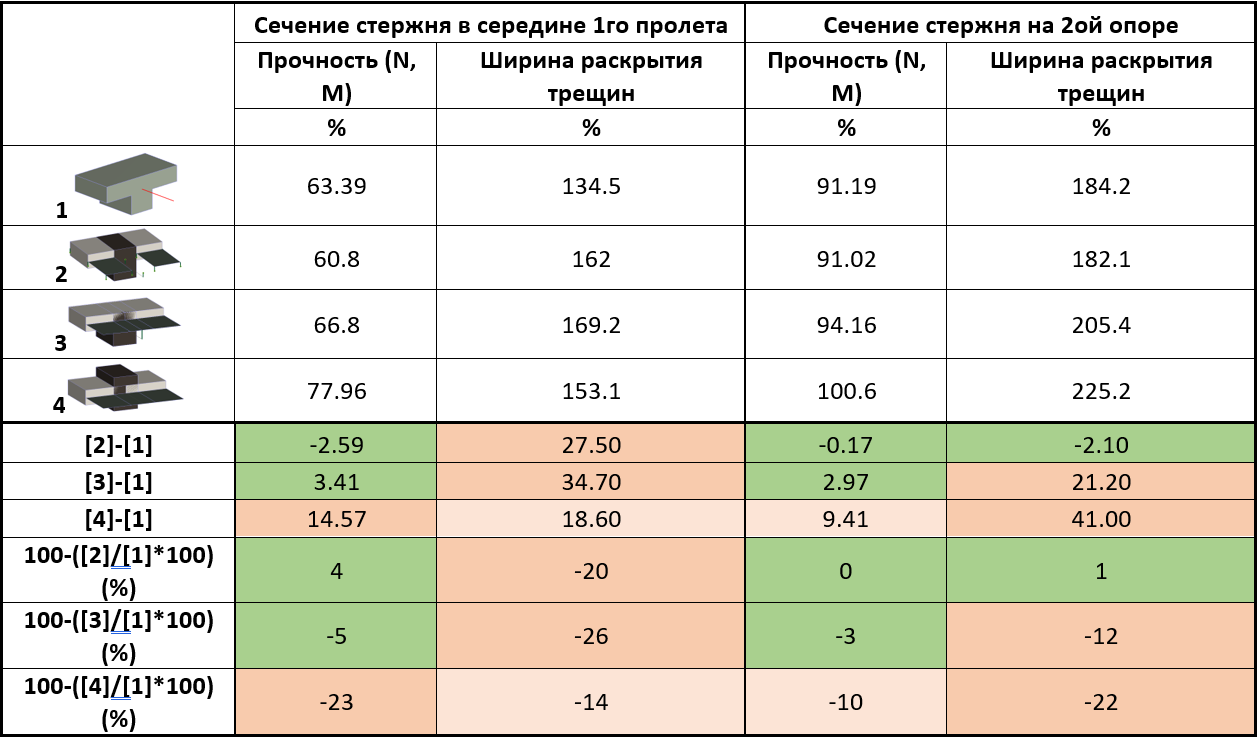
Таблица 6 Результаты проверки сечений от полученных усилий в нелинейном расчете
Полученные результаты показывают схожие значения результатов расчета 1, 2 и 3 схем по прочности. Схемы 2 и 3 имеют близкие значения по всем проверкам, как в пролете, так и на опорах.
Выводы
- Расчет балки в составе монолитного перекрытия следует выполнять с учетом физической нелинейности конструкций;
- Применение прямоугольной балки с жёсткой вставкой - наиболее оптимальный способ моделирования балки в составе монолитного перекрытия для расчетов каркасов зданий с учётом нелинейных свойств железобетона;
- Применение жестких вставок для железобетонных балок в составе монолитного перекрытия позволяют уменьшить и уточнить прогибы.
Примечание
- На разницу перемещений и напряжений в 1 и 2,3,4 влияет коэффициент Пуассона;
- Для нахождения наиболее корректных прогибов балки в нелинейном расчете следует задавать график работы материала для нормативных сочетаний нагрузок с учетом доли длительности, а также с учетом ползучести бетона;
- Результаты расчета пластинчатых элементов, поперечных сил и поперечной арматуры в балке в заметке не рассматривались.
Как вам материал? Задать вопрос или обсудить заметку можно на нашем форуме
Перейти на форум