Содержание:
- Исходные данные
- Создание пользовательских сечений
- Ручной расчет сечения
- Вывод
Данная заметка посвящена работе с модулем Сечения и проверке ручным способом полученных результатов из ЛИРА 10. Мы наглядно разберем, как работать со сталежелезобетоном, как рассчитывать конструкцию и на что необходимо обратить внимание. Вы узнаете, как моделировать пользовательское сечение и как проверить результаты расчета программы, если требуется.
Тема является продолжением заметки №22 Конструктор сечений, создание пользовательских сечений.
Исходные данные:
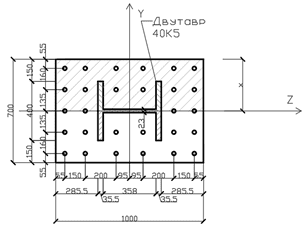
Сталежелезобетонная колонна среднего этажа рамного каркаса квадратного поперечного сечения с размерами по рис. 1. Длина колонны – 6,6 м, опирание шарнирное несмещаемое на одном конце и жесткое на другом. Бетон класса по прочности на сжатие В40. Жесткая арматура – двутавр 40К5 по ГОСТ Р 57837–2017 из стали С345. Стержневая арматура расположена по контуру согласно рис. 1 – 28шт. d20А500С. Строительство в г. Москве.
Создание пользовательских сечений
Для этого необходимо создать файл DXF с двутавром 40K5 (из сортамента). Далее, применив модуль «Сечения», задать геометрию и материалы сечения.
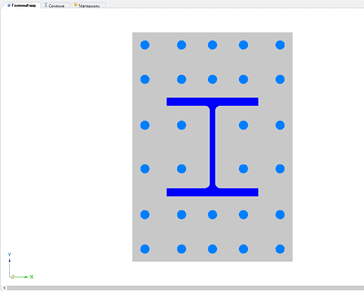
Рис. 1. Проект в модуле «Сечения»
Для того чтобы получить корректные нормальные усилия в расчетной модели, необходимо произвести расчет пользовательского сечения перед его экспортом в общую схему по примеру, описанному в заметке №22.
После выполнения расчета можно проанализировать результаты во вкладке «Таблица результатов»:
Рис. 2. Панель «Анализ и документирование», вывод результатов в таблицу
С помощью таблицы можно узнать как геометрические характеристики заданного сечения, так и жесткостные:
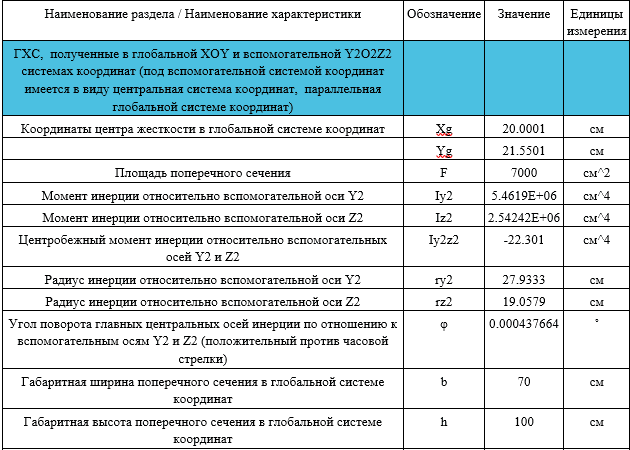
Рис. 3. Таблица результатов расчета сечения
После расчета можно экспортировать сечение в расчетную модель с помощью вкладки «Специальные» - «Импортированное сечение стержня». На рис. 4 видно, что также передаются и характеристики сечения в виде параметров:
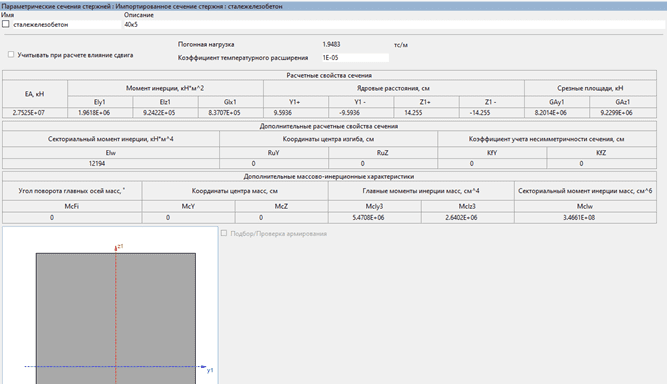
Рис. 4. Параметрический вид сечения с расчетными характеристиками
После расчета модели становится возможным применить усилия отдельно к сечению, чтобы проверить ручной расчет. Это можно сделать во вкладке «Специальные результаты»

Рис. 5. Панель «Специальные результаты»
Задав действующие нормальные усилия, можно оценить напряжения, как во всем сечении, так и отдельно в бетоне и стали:
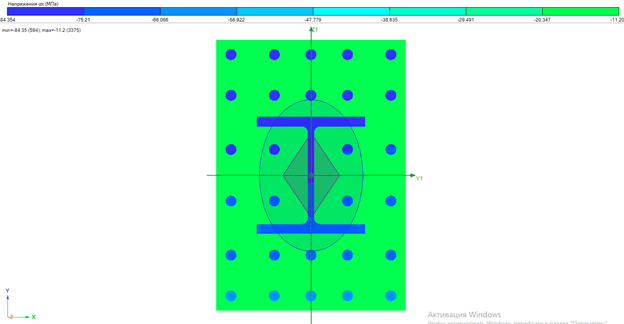
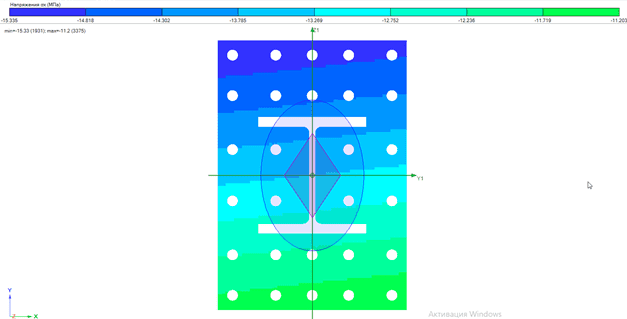
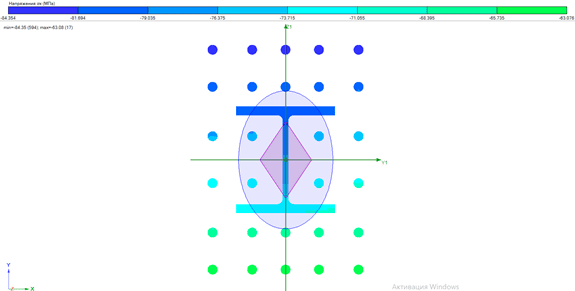
Рис. 6, 7, 8. Напряжения σх в элементе
Анализируя полученные данные можно вычислить коэффициент использования элементов.
Модуль сечения применим для создания сечений, не входящих в базу сортаментов, с дальнейшим экспортом в расчётную модель для получения корректных результатов расчета согласно примеру, описанному в заметке №22.
Используя полученные данные можно произвести ручной расчет сечения колонны согласно методическому пособию по расчету и проектированию сталежелезобетонных конструкций с жесткой арматурой
Ручной расчет сечения
Нагрузки:
- изгибающий момент в плоскости наибольшей жесткости двутавра
My = 313,0 кНм;
- изгибающий момент в плоскости наименьшей жесткости двутавра
Mz = 16,0 кНм;
- продольная сила N = 13730 кН.
Все нагрузки длительные.
Требуется проверить прочность поперечного сечения.
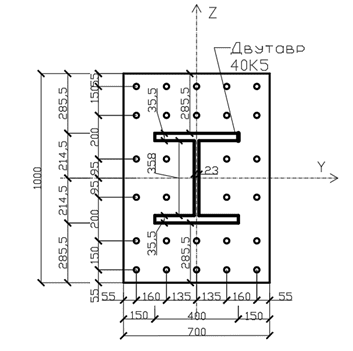
Рис. 9 - Геометрические размеры поперечного сечения колонны.
Записываем геометрические и прочностные характеристики элементов, формирующих поперечное сечение сталежелезобетонной колонны:
Ry= 310 Мпа | eb2= 0,0048 |
Rs= 435 Мпа | Ast= 37049 мм2 |
Rsc= 435 Мпа | bf1=bf2= 400 мм |
Rb= 22 Мпа | tf1=tf2= 35,5 мм |
Es= 200000 Мпа | tw= 23 мм |
Est= 206000 Мпа | hw= 358 мм |
Eb= 36000 Мпа | |
Площадь поперечного сечения одного стержня продольной арматуры равна 314,5 мм2.
Момент инерции одного стержня продольной арматуры относительно собственной оси Is1 = 7850 мм4.
Моменты инерции стального сердечника относительно собственной оси:
Iy,st = 120290,28 ∙ 104 мм4 , Iz,st = 37914,85 ∙ 104 мм4 .
С учетом длительности действия нагрузок расчетное сопротивление бетона осевому сжатию
Rb = yb1Rb = 0,9 ∙ 22,0 = 19,8 МПа.
Модуль деформации бетона с учетом длительности действия нагрузки определяем по формуле (Г.13) [3]
Eb1 = Eb,τ = Eb/(1 + φb,cr) = 36000 / (1+2,3) = 10909,09,
где φb,cr = 2,3 коэффициент ползучести бетона, принимается по [4] (таблица 6.12)
Определяем коэффициенты приведения к бетону для жесткой и гибкой арматуры по формуле Г.18 [3]:
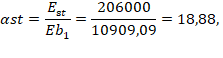
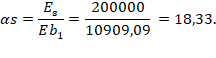
Выполняем проверку условия подпункта 7.1.1.3 [3]: 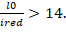
Радиус инерции приведенного сечения определяется по формуле Г.15 [3]:
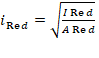
Вычисляем моменты инерции приведенного сечения элемента относительно его центра тяжести по формуле Г.16 [3]. В рассматриваемом примере центр тяжести приведенного сечения совпадает с центром тяжести бетонной части и жесткой арматуры в связи с их симметричным расположением, моменты инерции равны:
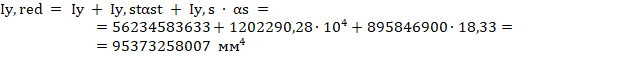
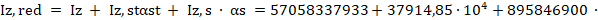
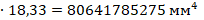
где Iy,s ,Iz,s – моменты инерции стержневой арматуры относительно центра тяжести приведенного сечения:
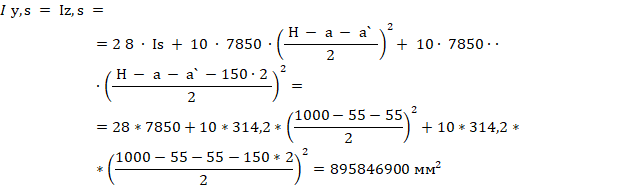
Iy,Iz – моменты инерции бетонной части относительно центра тяжести приведенного сечения (с учетом вытеснения бетона арматурой), определяемые по формулам:
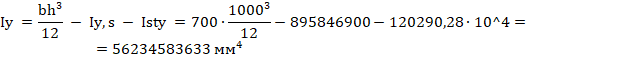
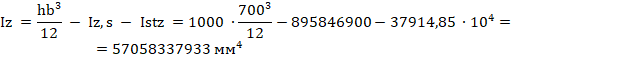
Определяем площадь приведенного поперечного сечения формуле Г.17 [3]:
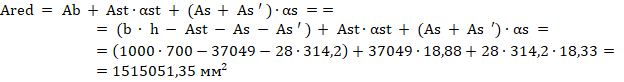
Радиус инерции приведенного сечения
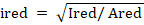
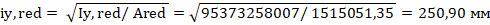
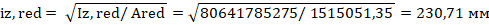
Расчетную длину элемента определяем по пункту 8.1.17 [4]:
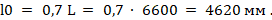
Тогда: 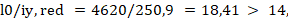
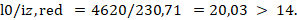
Согласно подпункту 7.1.1.3 [3], влияние прогиба на значение эксцентриситета следует учитывать.
Определение эксцентриситетов
Определим случайный эксцентриситет ea согласно подпункту 7.1.1.5 [3]:
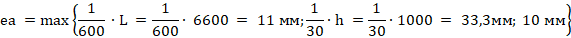
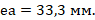
Определяем эксцентриситет e0 продольной силы для плоскостей y и z:
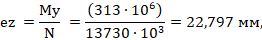
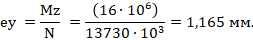
Для вычисления коэффициента, учитывающего влияние продольного изгиба элемента на его несущую способность η, необходимо определить характеристики приведенного сечения по Г.2 [3].
Коэффициенты:
- δe – относительное значение эксцентриситета продольной силы вычисляем по формуле
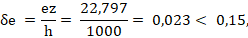
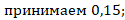
- φi – коэффициент, учитывающий влияние длительности действия нагрузки определяем по формуле
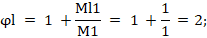
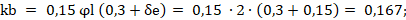
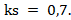
Определяем жесткость сталежелезобетонного элемента в предельной по прочности стадии (формула Г.11) [3]:
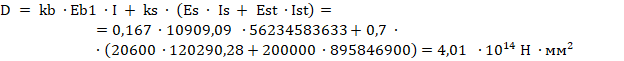
Условная критическая сила согласно [3] (формула (7.7))
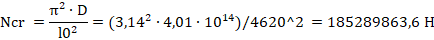
Коэффициент, учитывающий влияние продольного изгиба элемента на его несущую способность η, и определяемый по [3] (подпункт 7.1.2.5)
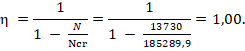
Определяем эксцентриситет приложения продольной силы относительно центра тяжести сечения растянутого стержня гибкой арматуры c учетом случайного эксцентриситета и влияния продольного изгиба согласно [3] (подпункт 7.1.2.4):
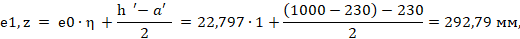
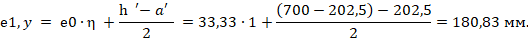
Проверка прочности поперечного сечения элемента в плоскости наибольшей жесткости z
Общий вид поперечного сечения элемента при проверке прочности в плоскости наибольшей жесткости приведен на рисунке 10.
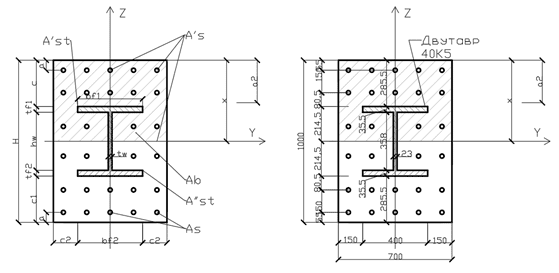
а – общий вид поперечного сечения; б – поперечное сечение – размеры и материалы
Рис. 10 – Проверка прочности поперечного сечения элемента в плоскости наибольшей жесткости z
Определяем граничную относительную высоту сжатой зоны для стального сердечника и стержневой арматуры согласно пункту 5.6 [2]:
- для стального сердечника:
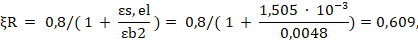
где 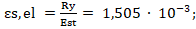
- для стержневой арматуры:
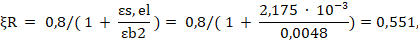
где 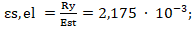
В качестве рабочего значения принимаем меньшее, как наиболее опасное ξR = 0,551.
Определяем высоту сжатой зоны сечения применительно к случаю расчета по формуле 6.3 [2]:
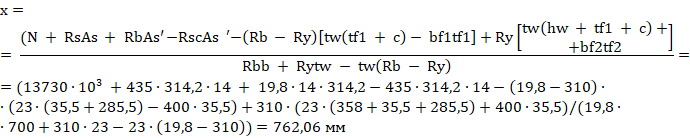
Определяем расстояние от центра тяжести растянутой арматуры до растянутой грани сечения
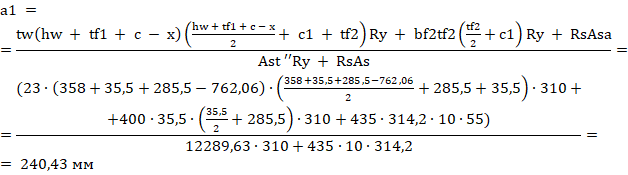
где 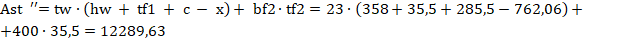 мм2.
мм2.
Рабочая высота сечения 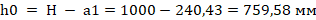 .
.
Определяем относительную высоту сжатой зоны
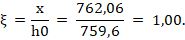
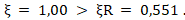
Условие ξ < ξR не выполнено, поэтому расчет высоты сжатой зоны необходимо выполнить по формуле 5.6 [2]:
Определяем высоту сжатой зоны сечения для случая ξ > ξR.
В качестве исходного значения высоты сжатой зоны будем использовать значение, полученное выше. Рабочую высоту сечения, площади сжатой и растянутой частей стального сердечника также принимаем по результатам выполненного выше расчета:
Высота сжатой зоны x определяется по формуле
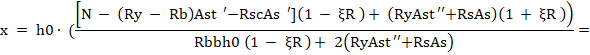
где 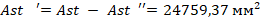 .
.
Полученное значение x значительно отличается от вычисленного ранее. Соответственно отличаются и остальные параметры, используемые в качестве исходных данных при записи уравнения. Необходимо выполнить дополнительную итерацию по корректировке значения высоты сжатой зоны.
Расстояние от центра тяжести растянутой арматуры до растянутой грани сечения a1 вычисляем по формуле:
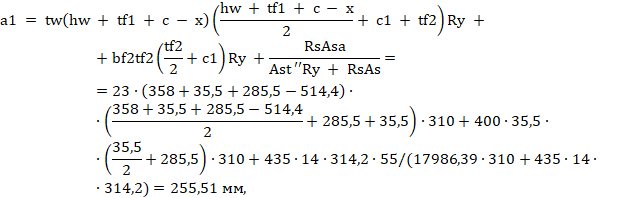
где 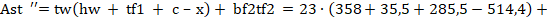
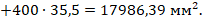
Рабочая высота сечения 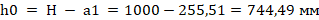 .
.
Площадь сжатой части жесткой арматуры
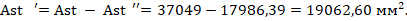
Высота сжатой зоны x определяется по формуле:
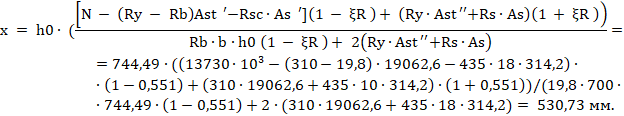
Для полученной высоты сжатой зоны определяем площади растянутой и сжатой частей жесткой арматуры:
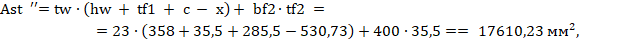
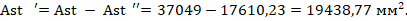
Полученное значение высоты сжатой зоны близко к значению, полученному на предыдущем этапе расчета (отличие 5%). Принимаем вычисленное значение x для дальнейших расчетов. В случае значительного отличия необходимо выполнить дополнительную итерацию по корректировке значения высоты сжатой зоны.
Определяем центр тяжести сжатого бетона относительно наиболее сжатой точки поперечного сечения.
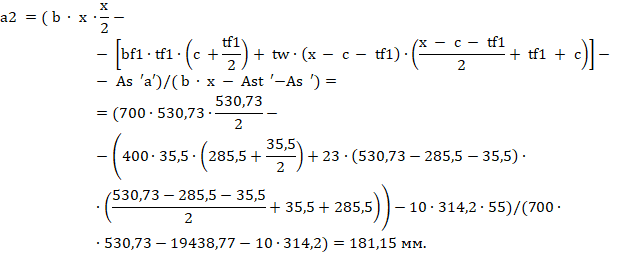
Определяем предельный момент, который может быть воспринят сечением элемента, относительно наиболее растянутого стержня гибкой арматуры
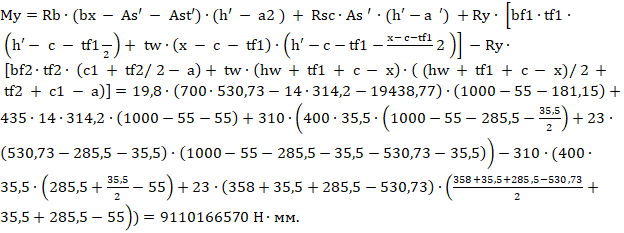 .
.
Отсюда предельная продольная сила, которая может быть воспринята сечением элемента при заданном эксцентриситете
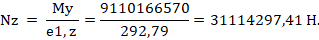
Проверка прочности поперечного сечения элемента в плоскости наименьшей жесткости y
Общий вид поперечного сечения элемента при проверке прочности в плоскости наименьшей жесткости приведен на рис.11.
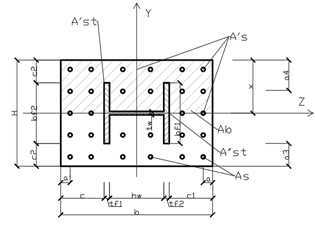
а – общий вид поперечного сечения; б – поперечное сечение – размеры и материалы
Рис. 11. Проверка прочности поперечного сечения элемента в плоскости наименьшей жесткости y
Определяем высоту сжатой зоны сечения применительно к случаю расчета 6.9 по формуле (6.5) [2]:
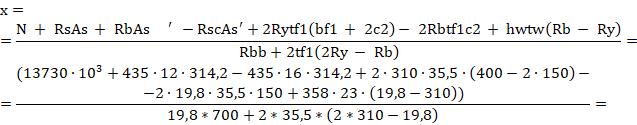
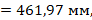
Полученный результат свидетельствует о том, что нейтральная ось не пересекает стенку двутавра, что соответствует принятой схеме расположения нейтральной оси в поперечном сечении. Необходимо выполнить перерасчет и уточнить значение высоты сжатой зоны.
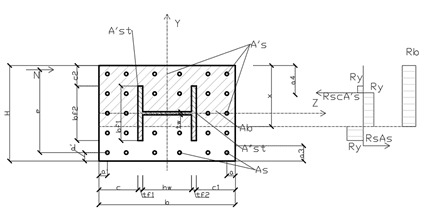
Рис. 12. Случай сжатия с изгибом в плоскости полок двутавра, когда нейтральная ось пересекает полки двутавра, стенка и более половины ширины полок сжаты
Принимаем x = 450 мм.
Центр тяжести растянутой арматуры a3 относительно растянутой грани сечения определяется по формуле
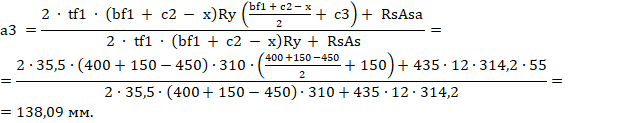
Рабочая высота сечения
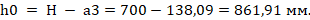
Определяем относительную высоту сжатой зоны 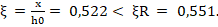
Условие ξ < ξR выполнено, поэтому расчет высоты сжатой зоны необходимо выполнить по формуле

Определяем центр тяжести сжатого бетона относительно наиболее сжатой точки поперечного сечения
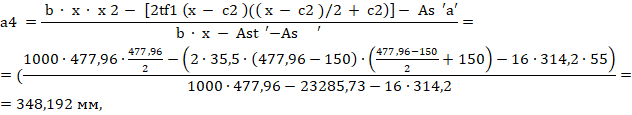
где 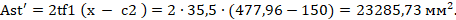
Определяем предельный момент, который может быть воспринят сечением элемента, относительно наиболее растянутого стержня гибкой арматуры
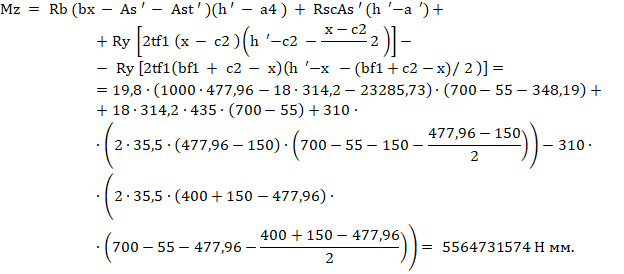
Отсюда предельная продольная сила, которая может быть воспринята сечением элемента при заданном эксцентриситете
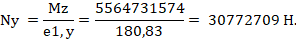
Определяем предельное значение продольной силы, которое может быть воспринято элементом согласно [3] (формуле (7.4)):
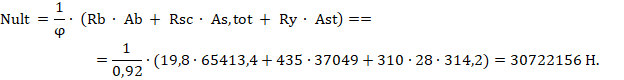
где φ = 0,92 согласно [3] (таблица 7.1);
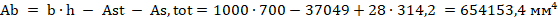 .
.
Выполняем проверку прочности по формуле (7.3) [3]:
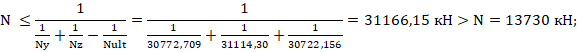
Коэффициент использования: kисп= 31166,15/13730 = 0,45
Коэффициент запаса: kзп= 13730/31166,15= 2,27
Прочность поперечного сечения колонны обеспечена.
Вывод
Расчетный комплекс ЛИРА 10 предоставляет широкие возможности для реализации инженерной мысли, и создание пользовательских сечений - одна из них. Это просто, удобно и понятно, как для опытного, так и для начинающего инженера. Использование модуля Сечения позволяет моделировать любые возможные сечения и позволяет не ограничиваться сортаментом.
Ручной расчет помогает проверить программу и лучше понять работу конструкции.
Список литературы
[1] Конструктор сечений, создание пользовательских сечений // Текст: электронный // Заметки эксперта ПК ЛИРА 10. – URL: https://lira-soft.com/wiki/notes/22-konstruktor-secheniy-sozdanie-polzovatelskikh-secheniy-rassmotrenie-funktsii-sozdaniya-i-importa-/
[2] Методическое пособие по расчету и проектированию сталежелезобетонных конструкций с жесткой арматурой. Министерство строительства и жилищно-коммунального хозяйства Российской Федерации. Федеральный центр нормирования, стандартизации и технической оценки соответствия в строительстве. Москва 2019 Текст: электронный. - URL: https://www.faufcc.ru/upload/methodical_materials/mp05_2019.pdf
[3] СП 266.1325800.2016 Конструкции сталежелезобетонные. Правила проектирования (с Изменением N 1, с Поправкой)
[4] СП 63.13330.2018 Бетонные и железобетонные конструкции. Основные положения. СНиП 52-01-2003 (с Изменением N 1)