Широкое применение оболочечных конечных элементов элементов при расчете пространственных конструкций побудило многих исследователей [2,3,4], в погоне за более точным результатом расчетов, к усовершенствованию классического подхода конечно-элементного анализа пластин и оболочек согласно теории Кирхгофа. Так были созданы теории Рейснера-Миндлина, учитывающие сдвиговые деформации и др. В целом, трудно определить, какая теория оболочек является наиболее выгодной, каждая имеет ряд своих допущений, которые формируют степень их применимости для расчета конструкций.
КЭ элемент тонкой оболочки, используемый в расчетах плоских и пространственных конструкций таких как: плиты перекрытия, стен, балки стенки и др, - согласно своей классической теории, имеет 5 степеней свободы в узле:
U – горизонтальное перемещение, положительное значение совпадает с направление местной оси элемента Х1.
V - горизонтальное перемещение, положительное значение совпадает с направление местной оси элемента Y1.
W – вертикальное перемещение (прогиб), положительное значение совпадает с направление местной оси элемента Z1.
UX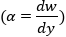 
– угол поворота относительно оси X1.
UY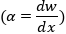 
– угол поворота относительно оси Y1.
Степени свободы U, V отвечают мембранным деформациям, а W,UX,UY изгибным. Данные узловые параметры определяют деформации элемента.
В общем случае функционал возможной работы внутренних сил КЭ пластины имеет вид:
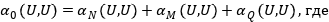
(1.1)
Функционал учитывающий влияние мембранной группы усилий:
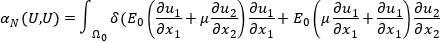
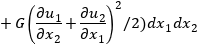
(1.2)
Функционал учитывающий влияние изгибной группы усилий:
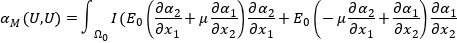
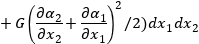
(1.3)
Функционал учитывающий влияние поперечного сдвига:
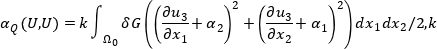
(1.4)
Функционал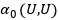 
не содержит поворота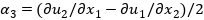 
Пользователи расчетных программных комплексов часто сталкивались с нехарактерными результатами расчетов при возникновении крутящего момента в элементах тонкой оболочки. Данный эффект хорошо визуализируется моделированием перемычек стержневыми КЭ при стыковке с элементами тонких оболочек стены (рис. 1). Такой узел примыкания по умолчанию будет считаться шарнирным, поскольку узлы стержневого конечного элемента имеют 6 степеней свободы, а элементы тонких оболочек 5. Для, получения корректного результата пользователю приходилось либо задавать АТТ по сечению стержневого КЭ, либо заводить стержневой КЭ в тело стены.
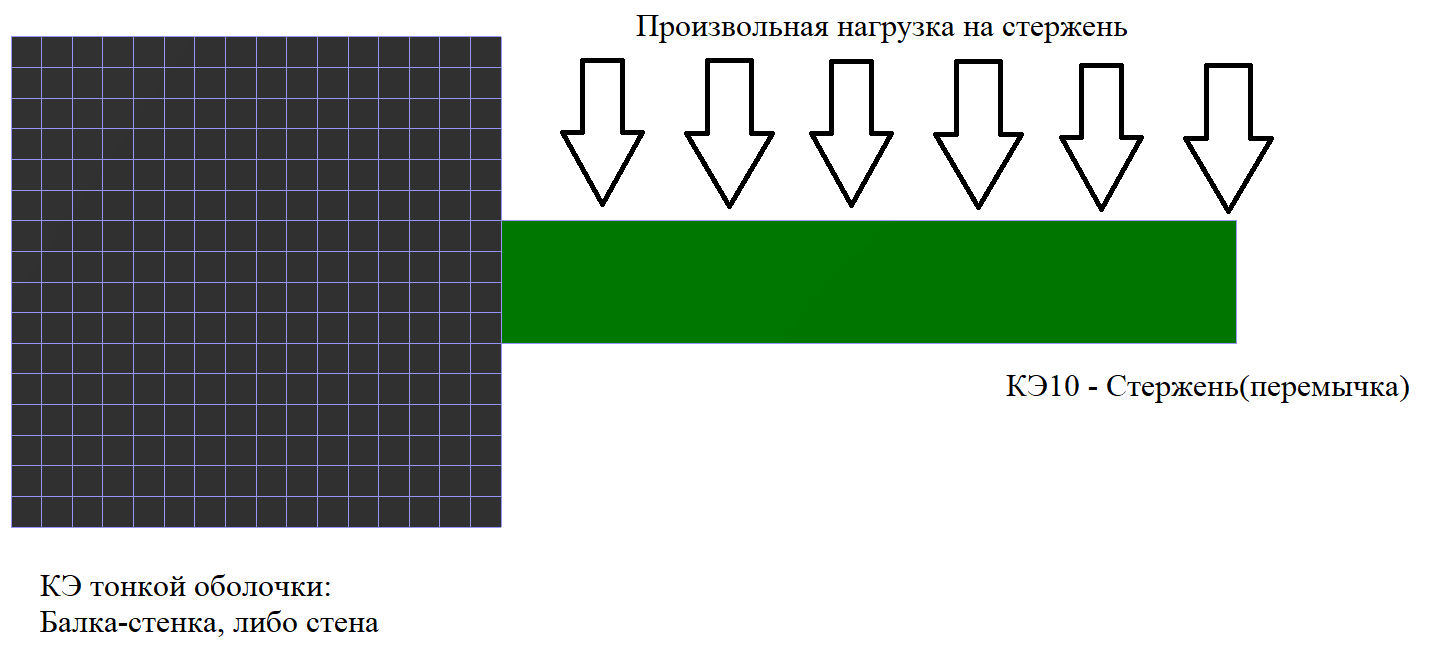
Рис.1 Расчетная ситуация примыкания балочного элемента к элементам тонкой оболочки.
В программном комплексе ЛИРА 10, реализован расчет оболочек с учетом 6(ой) степени свободы UZ(γ) – угол поворота относительно оси Z общей системы координат. Данная степень свободы появляется при стыковке элементов, не лежащих в одной плоскости, и необходима для учета пространственной работы конструкции.
В функционал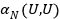 
(1.2), для учета поворота 
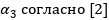, добавляется слагаемое:
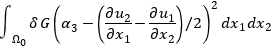
(1.5)
Активируется учет 6 степеней свободы в КЭ оболочки в основных параметрах расчета. Рассмотрим возможность использование поворотной степени свободы в КЭ оболочек при расчетах «реальных» конструкций в программном комплексе Лира 10.
Пример 1:
Стык пластинчатых элементов со стержневыми элементами (стыковка балочного элемента с диафрагмой).
В качестве расчетной модели принята жестко защемленная балка (рис.2).
Исходные данные:
Длина элемента 5 м.
Толщина пластины t=200мм.
Габариты балочного элемента B x H=200 x 200 мм.
Модуль упругости материала E=3,06e+6 т/м2
Коэф. Пуассона v=0.2
Сопряжение стержневого конечного элемента с элементами пластин стены (узел А) выполнено в 2 вариациях: сопряжение с заведение стержневых КЭ в элементы стены (А), обычное узловое сопряжение (Б).
Результаты расчета приведены в таблице 1 и на рис.3.
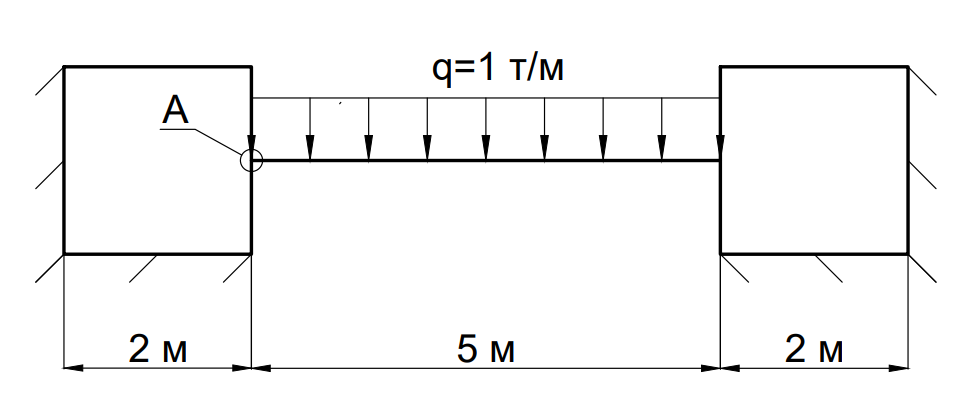
Рис.2 Расчетная схема жестко защемленной балки.
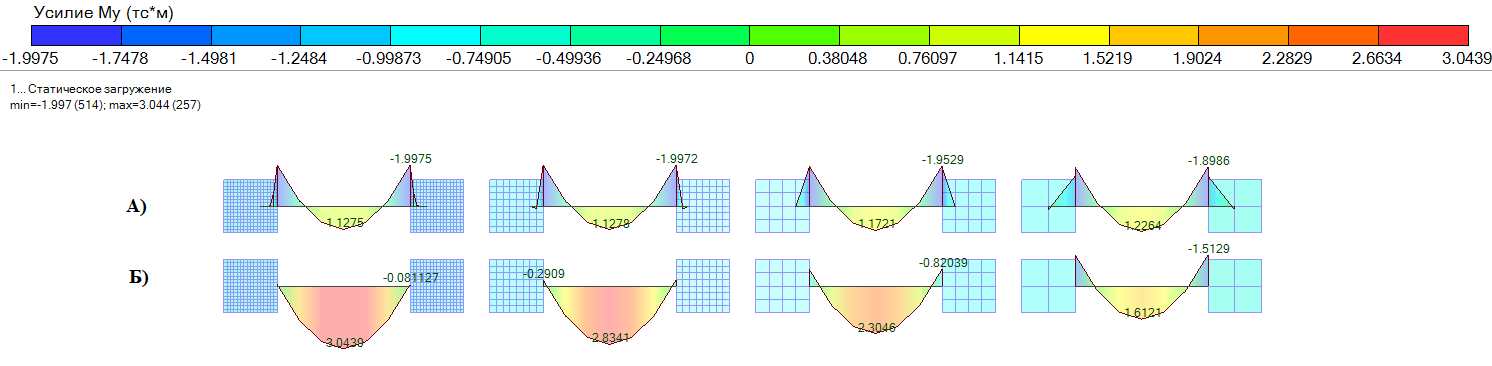
Рис.3 Эпюра изгибающих моментов My, при А) защемлении стержневого элемента; Б) обычном узловое сопряжении с шестью степенями свободы в узлах КЭ тонкой оболочки.
Таблица 1. Значения изгибающих моментов
Размер КЭ тонкой оболочки | My, тс*м примыкание типа (А) | My, тс*м примыкание типа (Б) | Аналитическое решение, тс*м | Погрешность(%), (А)/(Б) |
1х1 м | Опора | 1.90 | 1.51 | 2.08 | 9.47/37.75 |
Пролет | 1.23 | 1.61 | 1.01 | 17.88/37.26 |
0.5х0.5 м | Опора | 1.95 | 0.82 | 2.08 | 6.67/153.67 |
Пролет | 1.17 | 2.30 | 1.01 | 13.67/56.09 |
0.25х025 м | Опора | 2.00 | 0.3 | 2.08 | 4/593.3 |
Пролет | 1.13 | 2.83 | 1.01 | 10.62/64.3 |
0.125х0.125 м | Опора | 2.00 | 0.08 | 2.08 | 4/2500 |
Пролет | 1.13 | 3.04 | 1.01 | 10.61/66.77 |
Анализируя результаты, приведенные в таблице 1, можно сделать следующий вывод: сгущение сетки значительно влияет на результаты расчетов и может давать значения не соответствующие действительной работе конструкции. Расчетчику необходимо внимательно анализировать результаты, полученные как при использования 6-ти степеней свободы КЭ тонкой оболочки и без учета, при пространственной работе конструкций, поскольку имеет место зависимость от шага разбиения сети КЭ.
Пример 2:
Расчет свайного основания на действие сейсмического воздействия при использовании 6 степеней свободы в КЭ оболочек:
В качестве расчетной модели принята 24-этажная монолитно-каркасная пространственная конструкция, габаритами 18х18м, состоящая из ячеек(блоков) 6х6м, с лестнично-лифтовым узлом (ЛЛУ), см. рис.4.
Исходные данные:
Нагрузки:
Собственный вес (q=2.5 т/м3);
Постоянная распределенная нагрузка на плиту перекрытия 200 кг/м2;
Длительная распределенная нагрузка на плиту перекрытия 200 кг/м2;
Кратковременная распределенная нагрузка на плиту перекрытия 150 кг/м2 (полезная).
Сейсмическое воздействие для площадки сейсмичностью 9 балов (направляющий косинус Cx=1)
Модуль упругости E=3,06e+6 т/м2
Коэф. Пуассона v=0.2
Рис.4 Расчетная модель пространственной монолитно-каркасной конструкции.
При анализе результатов обратим внимание на эпюры крутящих моментов в КЭ оголовков свай и увидим, что при расчете с учетом 6 степеней свободы в элементах оболочек, значение крутящего момента Mx уменьшилось приблизительно на 16% для максимальных значений моментов на краевых сваях, сваях по контуру ЛЛУ, которые непосредственно контактируют со стержневыми элементами колонн. В сваях в зоне пролетов значения из нулевых и близких нулю значений многократно возрастают, за счет перераспределения крутящих моментов, при добавлении дополнительной поворотной степени свободы в пластинчатые элементы, моделирующие плиту ростверка (рис.5 и 6.).
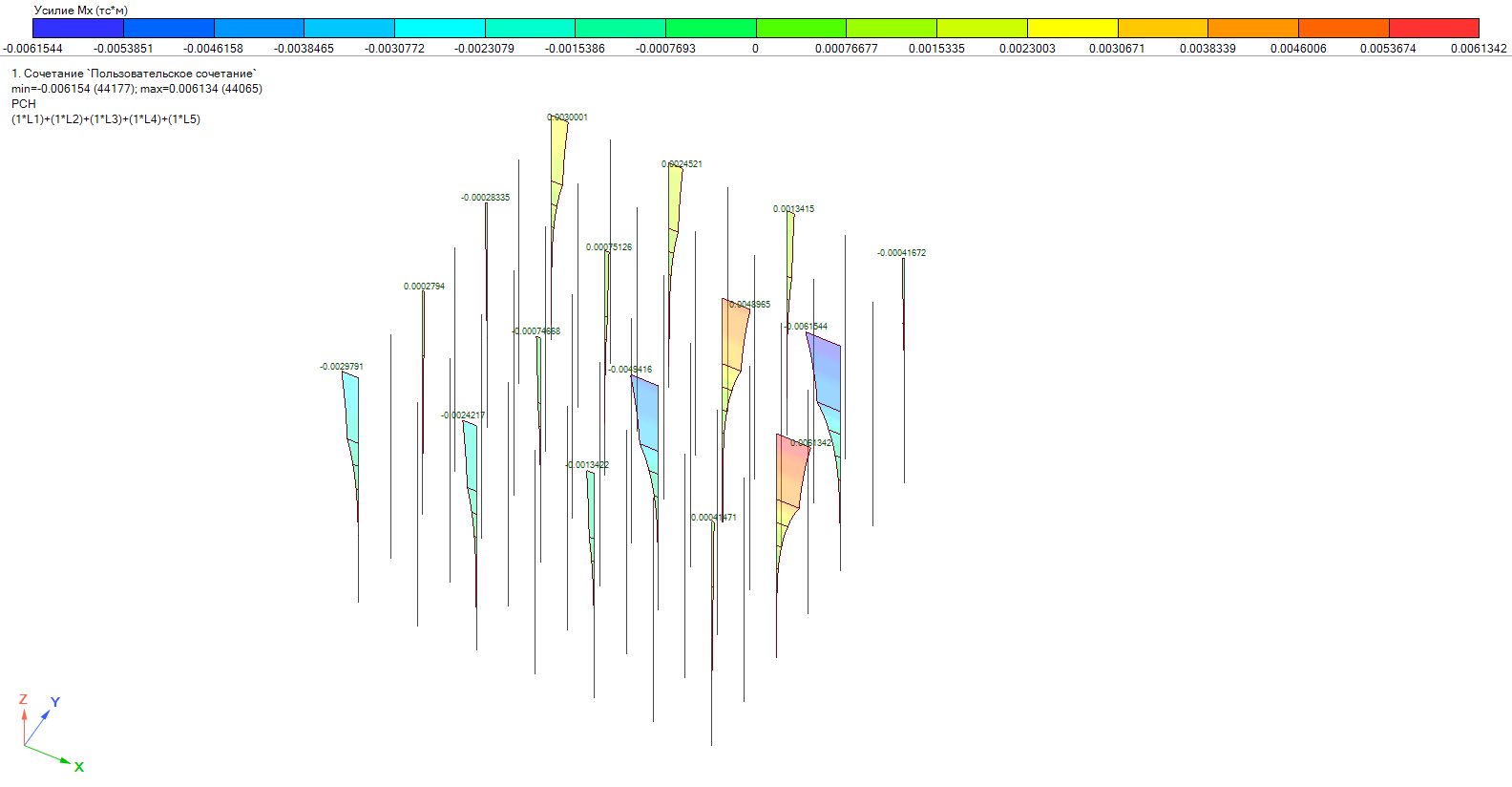
Рис.5 Эпюра крутящего момента в сваях Mx при расчете с классическими оболочками.
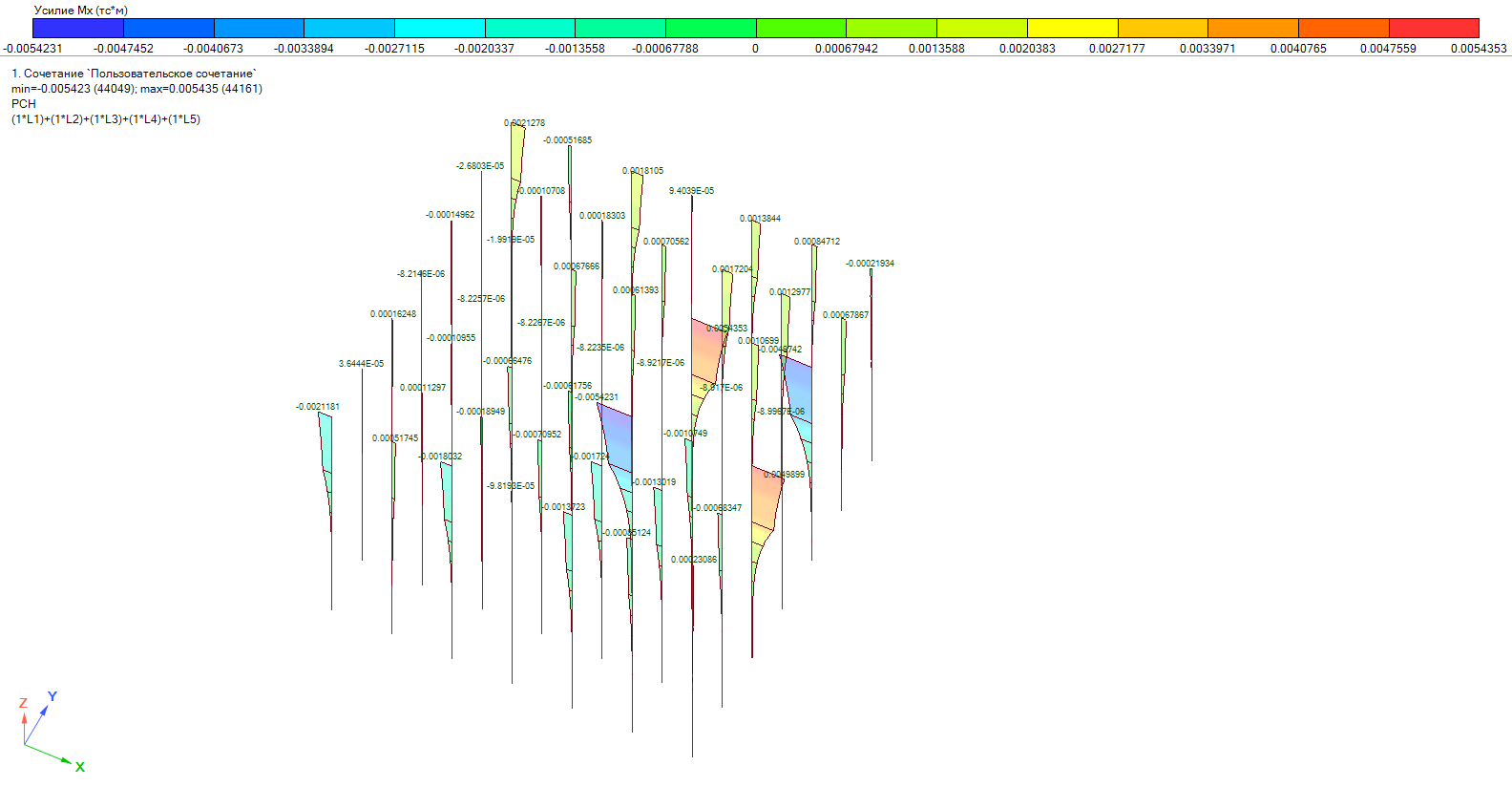
Рис.6 Эпюра крутящего момента в сваях Mx при расчете с оболочками, имеющими степень свободы UZ(γ).
Выводы:
- Проектировщику, применяя расчет с использованием 6 степеней свободы, нужно тщательно анализировать модель на соответствие полученных усилий в элементах, действительной работе конструкции. По возможности создавать локальные задачи для контроля сходимости результатов расчета.
- Необходимо сравнивать результаты расчета МКЭ и аналитических методов расчета.
- Применение 6 степеней свободы позволяет в большинстве задач избавиться от геометрической изменяемости системы, но при этом может приводить перераспределению усилий, отличающихся от сложившихся подходов к моделированию конструкций.
Список литературы:
- Программный комплекс ЛИРА 10.12. Руководство пользователя. 2021 год. 859 стр.
- Wilson EL, Ibragimbegovic. Thick shell and solid elements with independent rotation fields. — Int. J. Num. Meth. End. — 1991. — 31. — P. 1393-1414.
- Ibrahimbegovic, A.; Taylor, R. L.;Wilson, E. L. (1990): A robust quadrilateral membrane finite element with drilling degrees of freedom. International Journal for Numerical Methods in Engineering, vol. 30, pp. 445–457.
- H. Nguyen-Van, N. Mai-Duy and T. Tran-Cong. An improved quadrilateral flat element with drilling degrees of freedom for shell structural analysis. CMES, vol.49, no.2, pp.81-110, 2009.
Как вам материал? Задать вопрос или обсудить заметку можно на нашем форуме
Перейти на форум
