Н.Ю. ЦЫБИН1,2
1 НИУ МГСУ, 129337, Москва, Ярославское шоссе, 26
2 ООО «ЦПР Форма», 115114, Москва, 1-й Кожевнический пер., 10
science@nikitatsybin.ru
В большинстве опытов по испытанию адгезионных соединений измеряется средняя адгезионная прочность. Данная величина вычисляется как отношение разрушающей нагрузки к площади склейки. Подобный подход подразумевает равномерное распределение касательных напряжений. Исследователи давно обнаружили, что средняя адгезионная прочность соединения является сильной функцией геометрических [1] и физико-механических параметров модели и, следовательно, делает малоинформативными и несопоставимыми экспериментальные данные, выполненные на отличающихся образцах. Малочисленные результаты по измерению касательных напряжений по площади склейки с использованием преимущественно поляризационно-оптических методов [2] показывают, что распределение напряжений является нелинейной функцией. При этом наблюдается концентрация напряжений у торцов модели. В связи с этими фактами возникает необходимость детального изучения напряженно-деформированного состояния адгезионных соединений.
Постановка задачи
Рассмотрим многослойный стержень, состоящих из трех одинаковых слоев субстрата, скрепленных двумя слоями адгезива. Эскизный вид модели приведен на рисунке ниже.
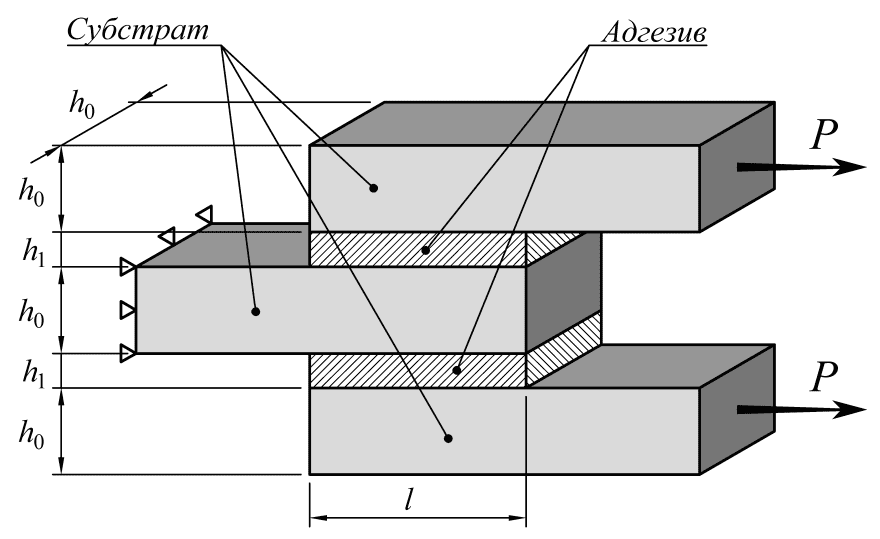
Рис. 1. Эскизный вид модели
В данной модели центральный слой субстрата закреплен левой гранью от горизонтальных смещений, правая его грань свободна. К двум внешним слоям справа приложена растягивающая нагрузка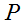 
.
Возникшая необходимость детального изучения напряженно-деформированного состояния потребовала от исследователей использования различных современных вычислительных методов. Одним из таких является метод конечных элементов.
Решение с использованием метода конечных элементов
Для решения данной задачи с использованием программного комплекса ЛИРА 10.8, реализующим метод конечных элементов, была создана плоская модель. На рисунке ниже приведен общий вид данной модели.
Рис. 2. Общий вид конечно-элементной модели без контактного слоя
На данном рисунке красные элементы – слои адгезива, зеленые – слои субстрата. Решалась упругая задача с признаком схемы №2 (плоская рама). Моделирование слоев адгезива и субстрата осуществлялось с использование пластинчатых конечных элементов №24, 27 (КЭ плоского напряженного состояния). В угловых точках было выполнено сгущение сети.
Ниже записаны физико-механические и геометрические параметры модели
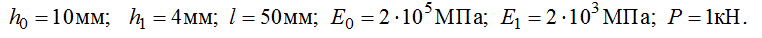
При моделировании использовался масштабный коэффициент 100.
Ниже приведены результаты вычисления нормальных и касательных напряжений в модели.
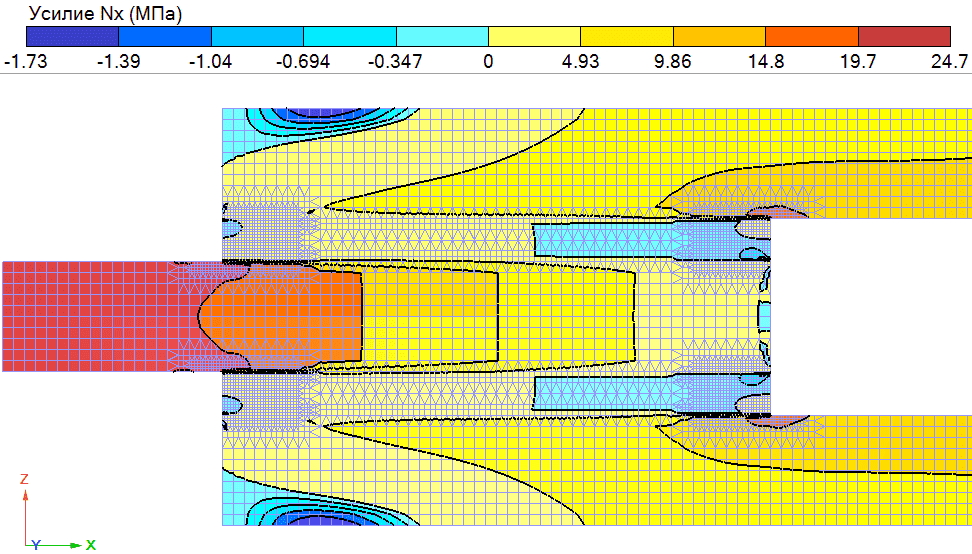
Рис. 3. Результат вычисления нормальных напряжений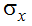 
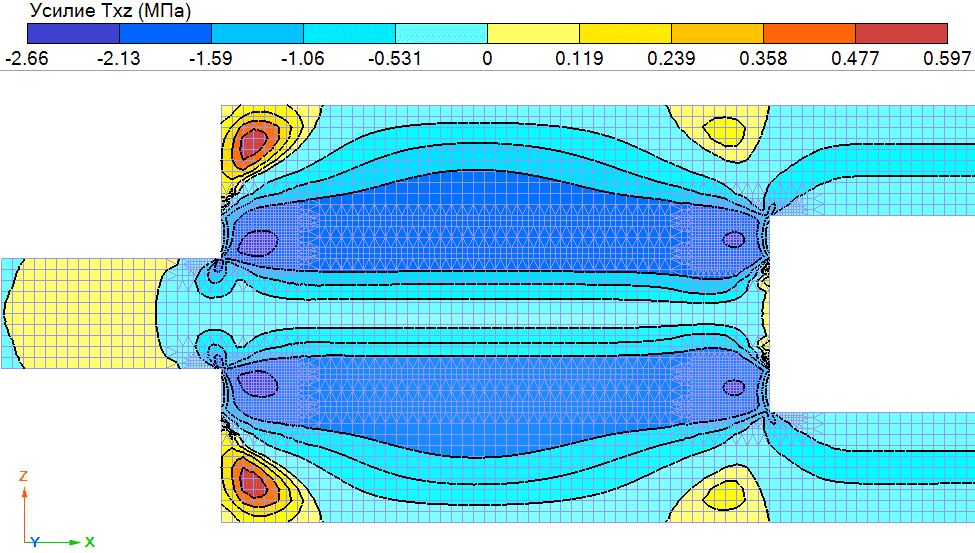
Рис. 4. Результат вычисления касательных напряжений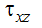 
Было установлено, что в угловых модели присутствует значительная концентрация напряжений. Наиболее наглядно это видно на изополях плотности энергии.
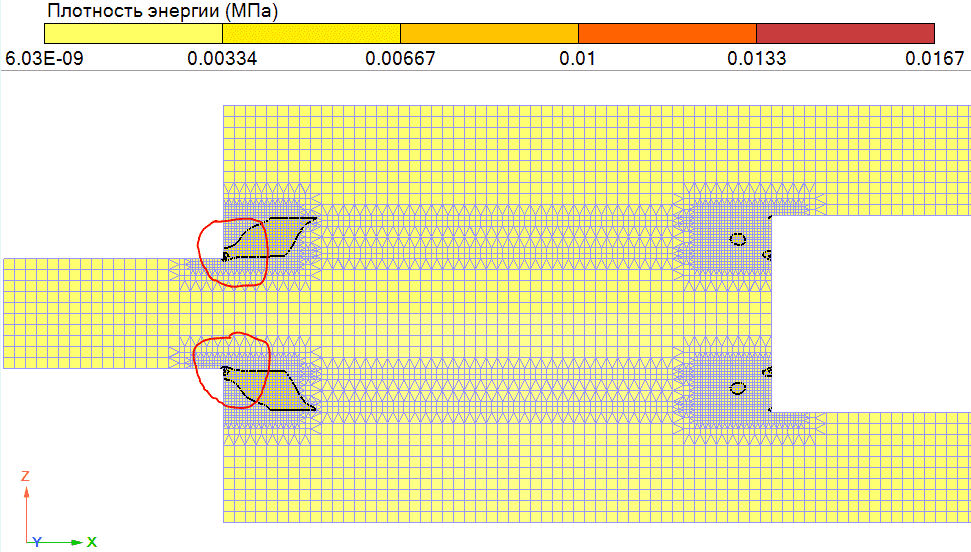
Рис. 5. Результат вычисления плотности энергии
Красным обведены зоны концентрации напряжений.
Далее было проанализировано влияние размеров конечных элементов на величину касательных напряжений в угловой точке и плотность энергии.
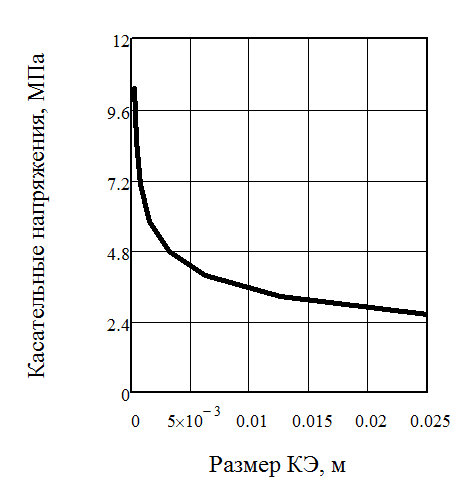
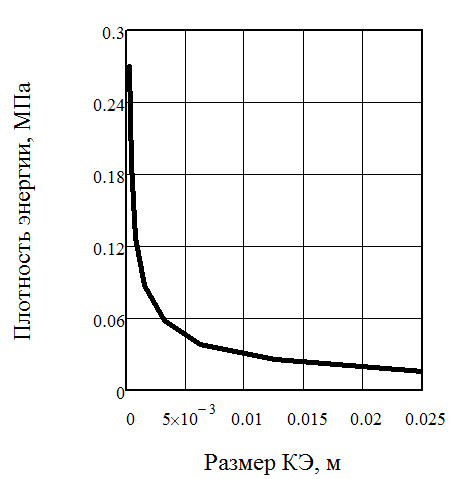
Рис. 6. Зависимость величины максимальных касательных напряжений и плотности энергии в зависимости от размера конечных элементов
Было установлено, что по мере уменьшения размера конечных элементов и приближения результатов численного расчета к точным результатам, величина плотности энергии и соответственно напряжений экспоненциально возрастала и стремилась к бесконечности. Схожие проблемы встречали другие исследователи.
Для исключения сингулярности в подобных задачах на данный момент используется два основных подхода.
- Использование физически-нелинейных моделей деформирования материалов.
- Добавление в угловые точки мениска [3], [4].
Первый подход помимо усложнения процесса моделирования, требует наличия диаграмм деформирования материала. Инженер же, как правило, таких данных не имеет. В любом случае реализация физической нелинейности требует от расчетчика углубленных знаний и опыта моделирования. Второй подход требует серьезного исследования геометрии мениска. Помимо этого, в реальной конструкции мениск может отсутствовать.
Другие подходы, как правило, являются математическими и их реализация в конечно-элементной модели либо невозможна, либо требует от авторов программного комплекса разработки отдельных маловостребованных расчетных модулей. Одним из дополнительных примеров является добавление по торцам модели «нерастяжимых» мембран.
Для решения данной задачи предлагается использовать модель контактного слоя [5], предложенную [6] и реализованную во многих работах Р.А. Турусовым. Контактный слой это трансверсально ортотропная среда, в которой происходит межмолекулярное взаимодействие слоев адгезива и субстрата.
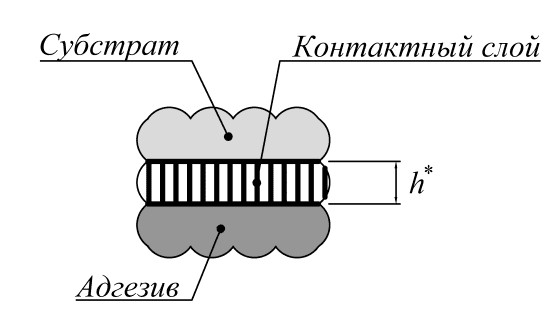
Рис. 7. Взаимодействие адгезива и субстрата через контактный слой
Параметры этой среды таковы, что ее можно абстрактно представить, как щетку коротких упругих стерженьков, не контактирующих между собой и ориентированных нормально к поверхности контакта. Так как стерженьки не соприкасаются, модули упругости данной среды в направлениях, перпендикулярных их боковой поверхности и коэффициент Пуассона равны нулю. В результате контактный слой имеет две основных характеристики, толщину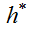 
и модуль сдвига 
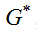, причем, так как коэффициент Пуассона равен нулю, модуль сдвига связан с модулем Юнга простым соотношением 
.
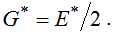Аналитическое решение рассматриваемой задачи с использованием модели контактного слоя и гипотез Эйлера-Бернулли для слоев адгезива и субстрата можно найти в [7]. Здесь же основной целью является демонстрация способа реализации модели контактного слоя в программном комплексе ЛИРА 10.8.
Рис. 8. Общий вид конечно-элементной модели с контактными слоями
На представленном рисунке контактные слои синего цвета. В остальном модель полностью соответствует рассмотренной ранее.
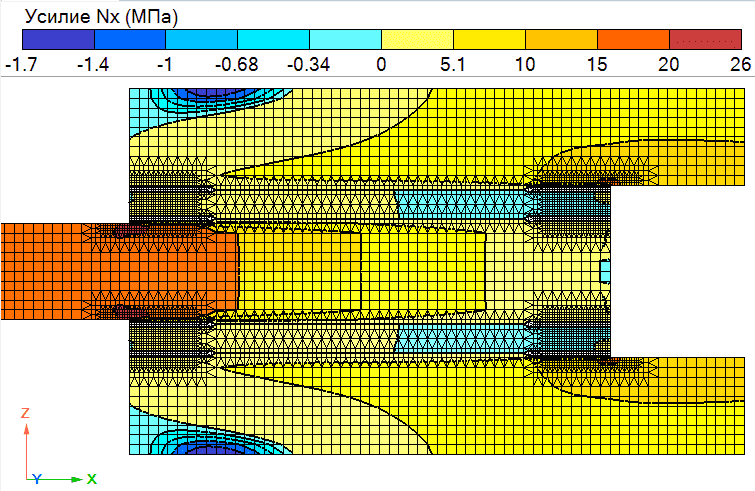
Рис. 9. Результат вычисления нормальных напряжений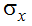
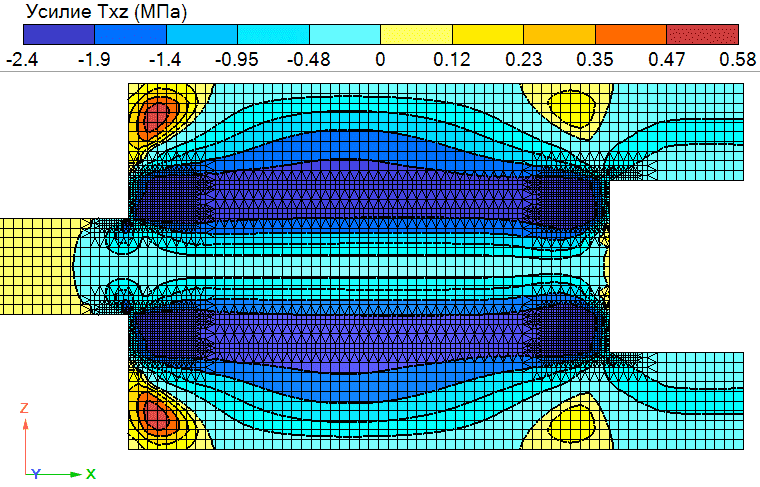
Рис. 10. Результат вычисления касательных напряжений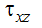
Рис. 11. Результат вычисления плотности энергии
Как видим, после добавления контактного слоя максимум касательных напряжений сместился от угловой точки. Для наглядности разместим рядом результаты вычисления касательных напряжений в окрестности данной точки для двух рассмотренных моделей.
 |  |
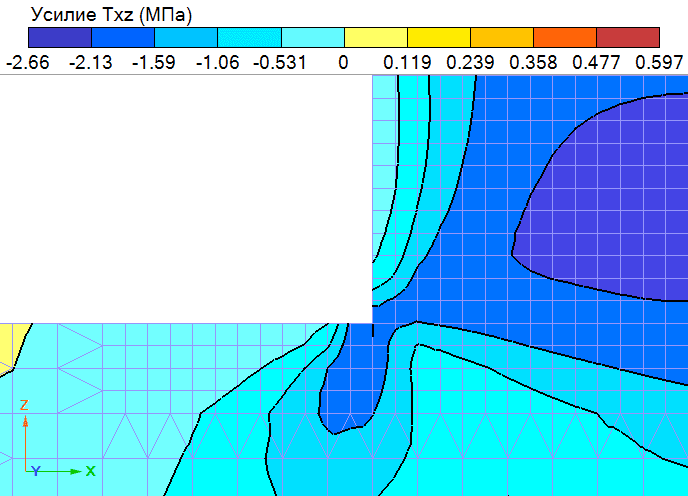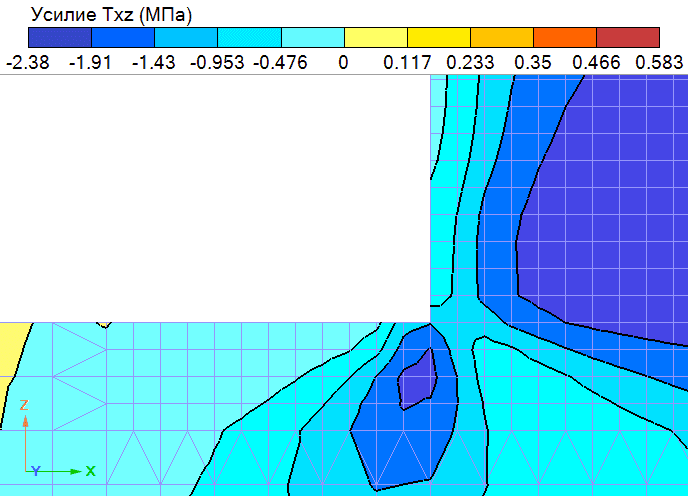Рис. 12. Касательные напряжения в угловой точке для модели без контактного слоя | Рис. 13. Касательные напряжения в угловой точке для модели с контактным слоем |
Далее проанализировано влияние размеров конечных элементов на величину максимальных касательных напряжений и плотность энергии для модели с контактным слоем.
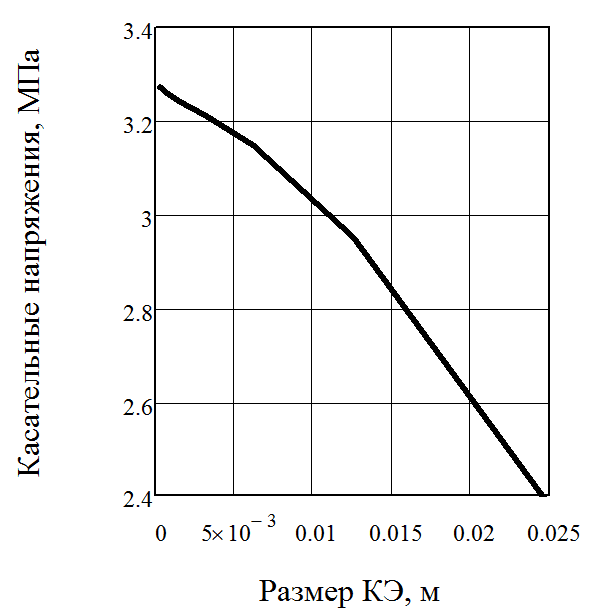
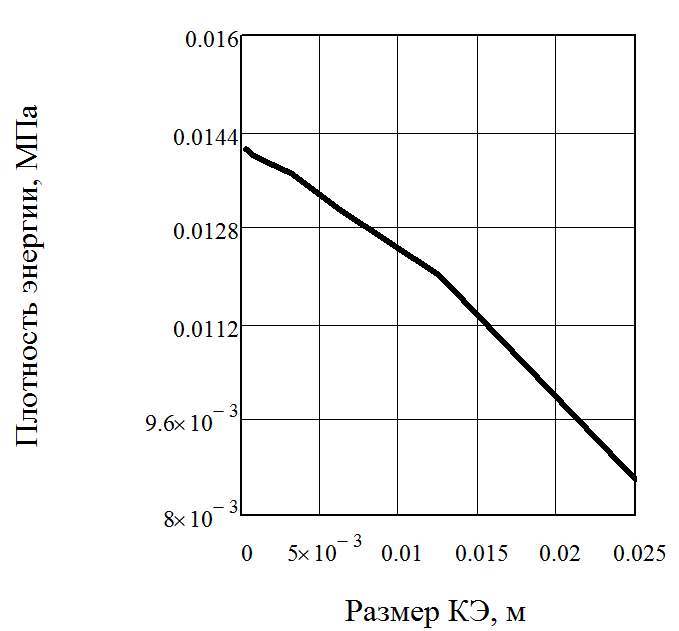
Рис. 14. Зависимость величины максимальных касательных напряжений и плотности энергии в зависимости от размера конечных элементов
Здесь мы видим существенно различный ход кривых представленных на Рис. 6и на данном рисунке. После добавления контактного слоя удалось избежать сингулярности касательных напряжений.
Приложение 1
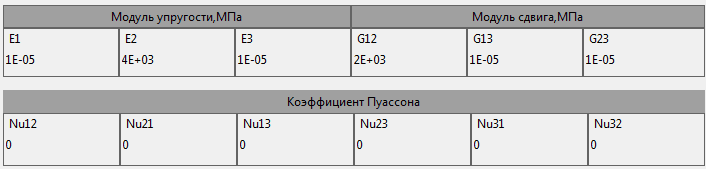
Рис. 15. Характеристики материала контактного слоя
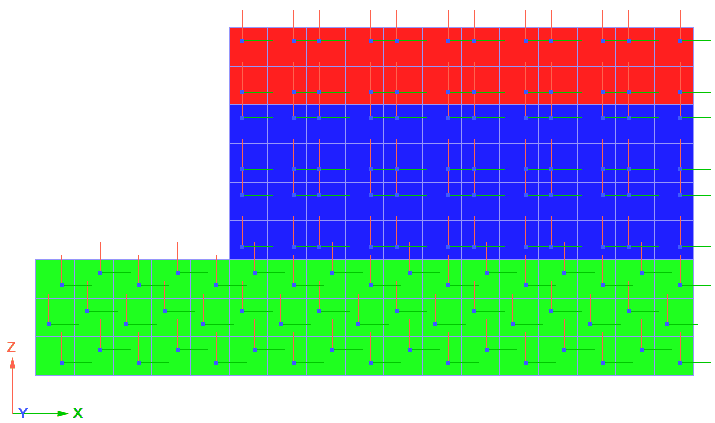
Рис. 16. Направление осей выравнивания напряжений и осей ортотропии
Заключение
В работе показано, что расчет адгезионных соединений в предположении абсолютно жесткого контакта слоев приводит к возникновению бесконечных напряжений. Показано, что для избегания данной проблемы эффективным способом является использование модели контактного слоя. Продемонстрирован простой метод реализации данной модели при расчете с использованием метода конечных элементов в программном комплексе ЛИРА 10.
Список литературы
- Lertora E., Campanella D., Mandolfino C., Gambaro C., Fratini L., Buffa G. Comparison Between FSW and Bonded Lap Joints – a Preliminary Investigation // AIP Conference Proceedings, Vol. 1896(1):110004, 2017.
- Туразян А.В., Рабинович А.Л. // ДАН СССР. 1970. Т. 194. № 6. С. 1305-1307.
- Calic A., Yildirim S. Effect of adherend recessing on bi-adhesively bonded single-lap joints // Sadhana, Vol. 42, No. 3, 207. pp. 317-325.
- Calic A. Effect of adherend shape on stress concentration reduction of adhesively bonded single lap joint // Engineering Review, Vol. 16, 2016. pp. 29-34.
- Турусов Р.А. Адгезионная механика: монография. 2-е изд. Москва: НИУ МГСУ, 2015. 232 с.
- Турусов Р.А., Вуба К.Т., Фрейдин А.С. Исследование влияния температурно-влажностных факторов на прочностные и деформационные свойства клеевых соединений древесины со стальной арматурой // Труды ЦНИИСК им. В.А.Кучеренко. 1972. № 24. С. 86-124.
- Andreev V.I., Turusov R.A., Tsybin N.Y. The contact layer method in calculating of the shear compounds // MATEC Web of Conferences, No. 117, 2017. pp. 1-7.
- Турусов Р.А., Вуба К.Т. Напряженное состояние и особенности оценки прочности адгезионных соединений при отрыве // Физика и химия обработки материалов, Т. 2, 1980. С. 108-115.
- Турусов Р.А., Маневич Л.И. Метод контактного слоя в адгезионной механике. Одномерные задачи. Сдвиг соединения внахлестку // Клеи. Герметики. Технологии, № 8, 2009. С. 2-12.
- Турусов Р.А., Маневич Л.И. Метод контактного слоя в адгезионной механике // Клеи. Герметики, Технологии. 2009. № 6. С. 2-11.
- Турусов Р.А., Маневич Л.И. Введение в адгезионную механику // Клеи. Герметики. Технологии, № 5, 2009. С. 2-8.
