Аннотация. С помощью современного программно-вычислительного комплекса ЛИРА 10.6 выполнена сравнительная оценка напряженно–деформированного состояния не поврежденного и коррозионно-поврежденного железобетонного элемента при динамическом и статическом нагружении. Проанализировано влияния ослабленного коррозией бетонного участка сжатой зоны на перераспределение напряжений в сечении.
Авторы:
Тамразян Ашот Георгиевич, д.т.н. профессор, зав. кафедрой ЖБК, Национальный Исследовательский Московский Государственный Строительный Университет (НИУ МГСУ)
Попов Дмитрий Сергеевич, аспирант, ассистент кафедры ЖБК, Национальный Исследовательский Московский Государственный Строительный Университет (НИУ МГСУ)
Воздействия агрессивных сред приводят к появлению коррозионных процессов, которые влекут за собой значительную деградацию несущей способности железобетонных элементов, зданий и сооружений в период их эксплуатации [1]. Длительная эксплуатация без проведения мероприятий по капитальному ремонту приводит к снижению конструктивной безопасности и живучести зданий. Задачи по уменьшению несущей способности при запроектных воздействиях и как следствие, прогнозирование рисков обрушений конструкций и зданий является актуальной задачей обеспечения безопасности строительных конструкций[2-4].
На современном этапе научной деятельности данных о принципах расчета, уровне действующих напряжений и возникающих деформациях в коррозионно-поврежденных железобетонных элементах при динамическом нагружении недостаточны.
Цель данной работы состоит в определении напряженно–деформированного состояния коррозионно–поврежденной изгибаемой балки, определения перемещений, влияние ослабленного бетонного участка на перераспределение напряжений в сечении при динамическом нагружении элемента.
Для определения напряженно-деформированного состояния по всему сечению элемента с учетом коррозионного повреждения смоделирована железобетонная балка из объемных восьмиузловых конечных элементов. Бетон выполнен из конечных элементов размером 25х25х50мм, арматура 20х12,7х50мм, что соответствует эквивалентной площади арматуры диаметром 18мм.
Железобетонная балка принята длиной 2,0м, шириной 0,3м, высотой 0,6м и армирована двумя стержнями диаметром 18мм в растянутой зоне сечения.
Исходя из принципов задания жесткостей приняты линейные изотропные материалы, где бетон класса В25 с модулем упругости Еb=30х103МПа, арматура класса А400 с модулем упругости Еs=2х105 МПа.
Следствием постоянного воздействия агрессивных сред на железобетонный элемент, является коррозионные повреждения арматуры и бетона. В результате происходит снижение прочностных характеристик материалов. В рассматриваемом случае коррозионные повреждения смоделированы в средней по длине части балки. Рассматриваемое повреждение принято размерами 0,5х0,3х0,11м (рис.1). Прочностные характеристики поврежденной бетонной части сечения приняты с модулем упругости Еb=10х103МПа, что примерно соответствует бетону класса В5.
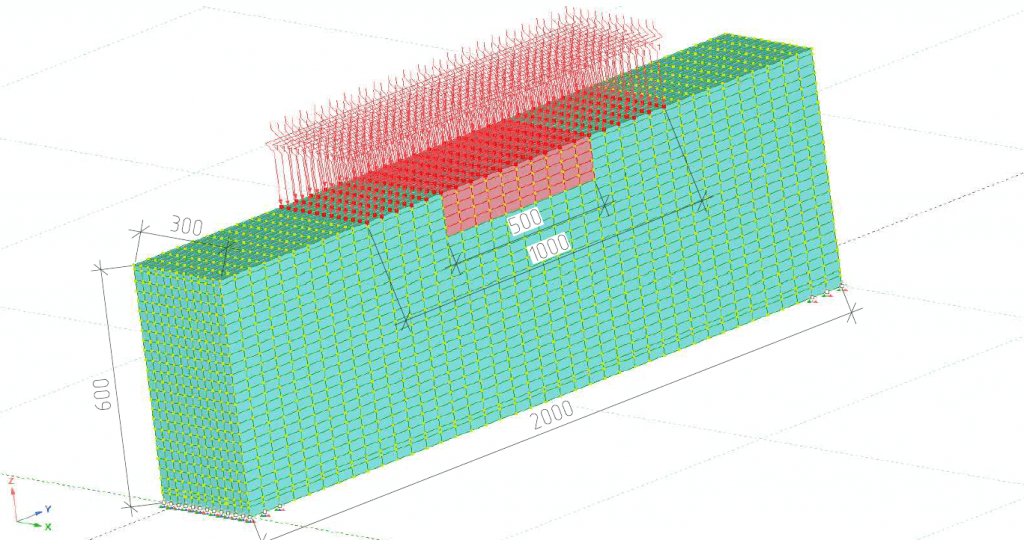
Рисунок 1 – Модель железобетонной коррозионно–поврежденной балки при динамическом воздействии
На железобетонный элемент воздействуют две статические нагрузки - собственный вес и равномерно распределённая нагрузка интенсивностью 40т/м2. Так же воздействует динамическая нагрузка, моделируемая ударом в средней части пролета балки размером 1,0м. Приложен одиночный удар со скоростью в 0,04сек., интенсивностью 1,0т (рис. 1). Применяемая динамическая нагрузка может возникнуть по причине обрушения вышележащей плиты перекрытия в результате аварийной ситуации.
Расчет на динамические нагрузки выполнен с использованием модуля «Динамика +». Данный модуль позволяет оценить напряженное-деформированное состояние в интересующий период времени, а также определить в какой момент времени возникают максимальные растягивающие и сжимающие напряжения в объемных конечных элементах.
Динамический расчет произведен с применением модального анализа, который позволяет определить формы и частоты собственных колебаний конструкции. По результатам модального анализа приняты первая и вторая форма колебаний, соответственно 102,81Град/с и 230,15Град/с частоты собственных колебаний, которые в свою очередь необходимы для учета демпфирования.
Формирование матриц масс для динамического нагружения выполнено из статических загружений. Для анализа напряженно–деформированного состояния в момент и после приложения ударной нагрузки, период фиксации напряжений и деформаций принят 5 секунд.
Максимальные нормальные напряжения Nx, Ny, Nz возникают в момент удара (0,04 сек). Для наглядности представлены графики максимальных растягивающих (знак +) и сжимающих (знак -) напряжений во времени для объемного конечного элемента «бетон» (рис. 2-4), расположенного в сжатой части сечения и объемного конечного элемента «арматура», расположенного в растянутом сечении (рис. 5-7). Рассматриваемые конечные элементы находятся в середине сечения, где возникают максимальные напряжения относительно всей балки. Указанные конечные элементы, как и железобетонная балка в целом имеет первоначальные механические характеристики материала (без коррозионного повреждения).
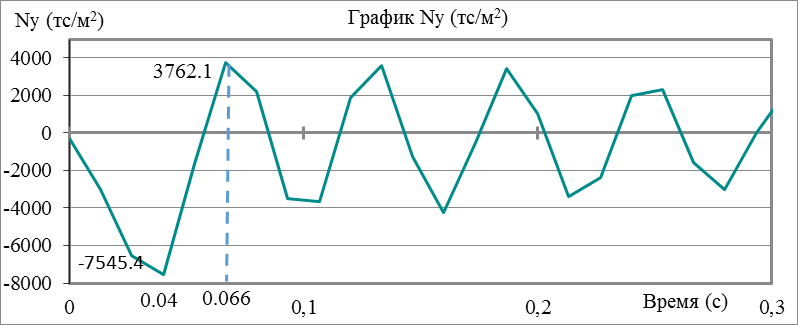
Рисунок 2. Нормальные напряжения Ny в объемном конечном элементе «бетон»
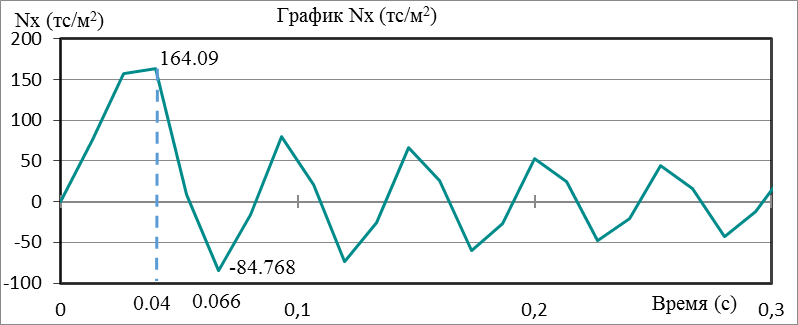
Рисунок 3. Нормальные напряжения Nx в объемном конечном элементе «бетон»
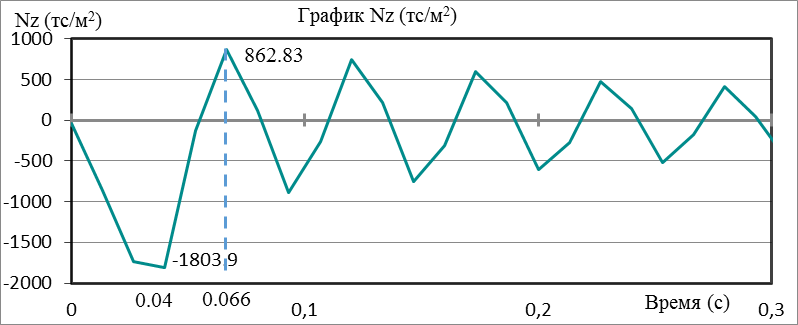
Рисунок 4. Нормальные напряжения Nz в объемном конечном элементе «бетон»
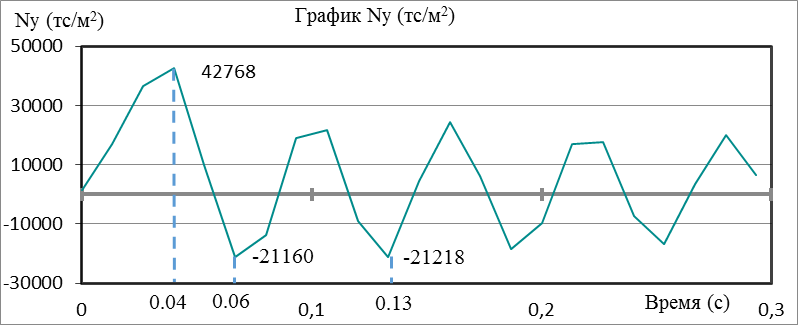
Рисунок 5. Нормальные напряжения Ny в объемном конечном элементе «арматура»
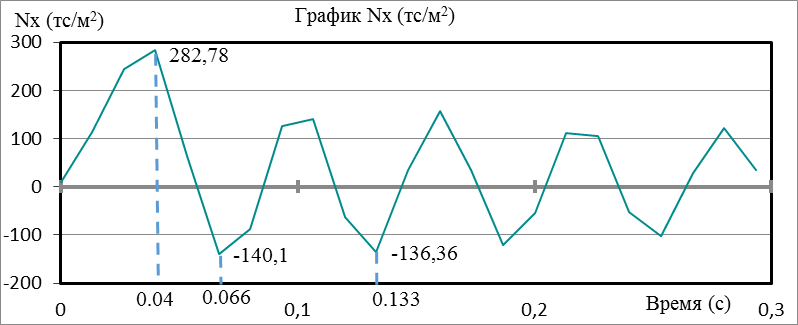
Рисунок 6. Нормальные напряжения Nx в объемном конечном элементе «арматура»
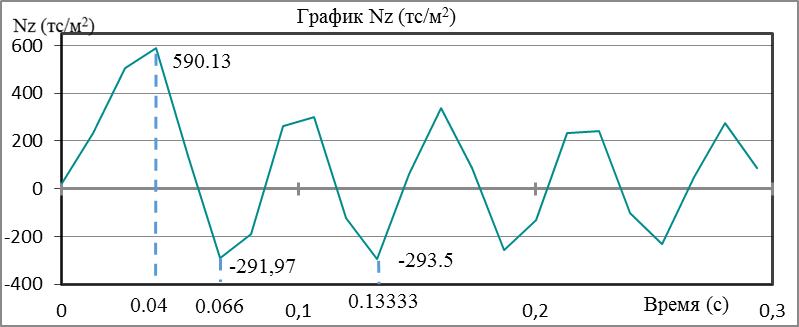
Рисунок 7. Нормальные напряжения Nz в объемном конечном элементе «арматура»
Проанализировав графики нормальных напряжений в объемном конечном элементе «бетон» можно сделать вывод, что максимальные напряжения сжатия Ny, Nz возникают на 0,04 секунде, что происходит в момент пика ударной нагрузки, экстремальные напряжения растяжения наблюдаются на 0,066 секунде. Напряжения Nx, возникающие на 0,04 секунде, являются растягивающими, а на 0,066 секунде сжимающими.
Графики нормальных напряжений в объемном конечном элементе «арматура», дают несколько отличную картину от графиков напряжений в бетонном элементе. Так максимальные нормальные растягивающие напряжения Ny, Nz, Nx возникают на 0,04 секунде. Экстремальные сжимающие напряжения Ny и Nz наблюдаются на 0,133 секунде. Здесь следует заметить, что на 0,066 секунде возникают достаточно близкие к максимальным по величине усилиям на данных площадках. При этом максимальные сжимающие напряжения Nx возникают на 0,066 секунде, а близкие по величине усилия на 0,133 секунде.
На рисунке 8 показаны максимальные растягивающие и сжимающие напряжения Ny от статического нагружения, в элементе «А» частично повреждённом коррозией железобетонном элементе в сжатой зоне и не поврежденном элементе «В».
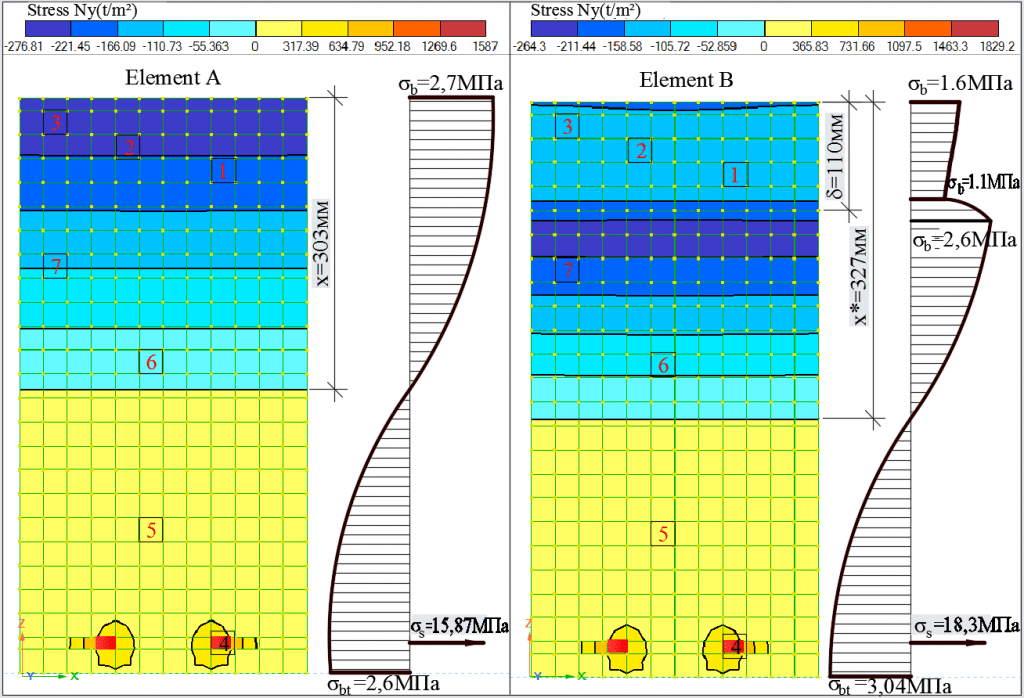
Рисунок 8. Эпюры напряжений в сечении, нормальном к продольной оси изгибаемого коррозионно–поврежденного и неповрежденного железобетонного элемента
При сравнении значений отмечено, что в поврежденном элементе напряжения в растянутой зоне больше, чем в неповрежденном элементе, а напряжения в сжатой зоне меньше. Данный факт объясняется тем, что прочностные характеристики прокорродированной части сечения снизились, тем самым постоянные действующие напряжения от внешней нагрузки перераспределяются, увеличиваясь в растянутой части сечения.
Эпюра нормальных напряжений в сжатой части сечения коррозионно–поврежденного элемента имеет скачкообразную форму, увеличение напряжений происходит на границе поврежденного и неповрежденного бетона (рис.8).
Высота сжатой зоны коррозионно–поврежденного элемента х* больше на 24мм, относительно высоты сжатой зоны х неповрежденного элемента. Многочисленное количество работ, посвященных коррозионным повреждениям железобетонных элементов выполнено Бондаренко В.М. [5,6], в которых говориться об увеличении высоты сжатой зоны и критериях ее нахождения.
В работе [6] представлена схема напряженного состояния нормального поперечного сечения коррозионно–поврежденного элемента (рис.9).
Рисунок 9. Схема напряженного состояния нормального поперечного сечения, поврежденного коррозией изгибаемого железобетонного с единичным армированием
На рисунке 9 обозначены А - зона полного коррозионного разрушения бетона (z*); Б - зона неполного коррозионного повреждения бетона (δ); В – зона неповрежденного бетона (р); а, b, х*, h, h0 - геометрические размеры бетонного тела (образца); К* - кривая функции повреждений (коэффициент сохранения исходных механических характеристик); Fz* – величина утерянной части силового сопротивления, обусловленная разрушением зоны А; F1 – величина утерянной части силового сопротивления, обусловленная снижением силового сопротивления в зоне Б; F2 – величина сохранившейся части силового сопротивления в зоне Б; Fs – величина силового сопротивления поврежденной коррозией расчетной арматуры Аs0; ωs – коэффициент коррозионного повреждения арматуры.
Опуская выкладки работы [5], сохранившиеся силы сопротивления в железобетонном элементе представляют вид:
Моментные плечи сил F2 и Fn относительно центра тяжести растянутой арматуры:
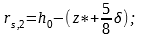 | 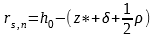 | (2) |
Предельный изгибающий момент силового сопротивления в сечении с учетом коррозионных повреждений:
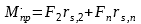 | (3) |
Высота сжатой зоны коррозионно–поврежденного элемента:
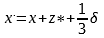
| | (4) |
Высота не поврежденного бетона сжатой зоны:
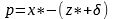 | | (5) |
Определим предельный изгибающий момент согласно (1-5), с условиями: х=30,3cм и δ=11cм (рис. 8); b=30см; h0=57см; z*=0; ωs=1, класс бетона В25, Rb=14.5МПа:
Определим М*пр по [7] с учетом частичного коррозионного повреждения сжатой зоны бетона по условиям: δ=11см с расчетным сопротивлением сжатию R*b=2.8МПа (класс В5); прочность неповрежденного бетона Rb=14,5МПа (класс В25); высота сжатой зоны коррозионно–поврежденного элемента х*=32,7см (рис.8); h0=57см; b=30см. ;
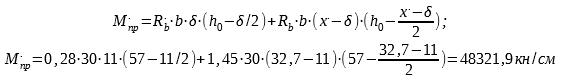 | (9) |
При сравнении критериев для нахождения предельного изгибающего момента, можно сказать, что в работе [5], в сжатой зоне бетона Б(рис.9) исключается 1/3 часть площади коррозионно - поврежденного бетона (δ), сохранившаяся площадь бетона принимается с первоначальными прочностными характеристиками и умножается на соответствующие моментные плечи до центра тяжести растянутой арматуры, высота сжатой зоны определяется по (4). В работе [7] площадь коррозионно – поврежденной сжатой зоны бетона Б(рис.9) не изменяется, но в расчет принимается с сниженными прочностными характеристиками, а высота сжатой зоны определяется из данных программного комплекса (рис.8).
Кроме снижения несущей способности железобетонного элемента в результате коррозионных процессов, возникает риск хрупкого разрушения, вследствие увеличения высоты сжатой зоны, что произойдет при не выполнении условия:
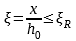 | | (10) |
Где ξ – относительная высота сжатой зоны; ξR – граничная относительная высота сжатой зоны, значение которой зависит от класса арматуры; х – высота сжатой зоны; h0 – рабочая высота сечения.
Проверим условие (10) для коррозионно – поврежденного элемента по [5], где ξR=0,531 соответствует арматуре класса А400.
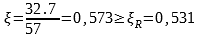
| | (11) |
Условие (10) не соблюдается, следовательно, произойдет хрупкое разрушение элемента.
Напряжения σ1, σ2, σ3 это частный случай нормальных напряжений, они действуют на главных площадках. Нормальные напряжения Ny, Nz, Nx на главных площадках принимают экстремальные значения.
Для объемных конечных элементов №1-3, расположенных в сжатой зоне сечения, коррозионно-поврежденного и неповреждённого элемента (рис.8), приведены главные напряжения, и соответствующие им деформации в таблицах 1 и 2 в динамической, и статической постановке соответственно.
Таблица 1. Главные напряжения и соответствующие им деформации при динамическом нагружении
Не поврежденные объемные конечные элементы |
№ | σ1 min (т/м2) | σ1 max (т/м2) | σ2 min (т/м2) | σ2 max (т/м2) | σ3 min (т/м2) | σ3 max (т/м2) | τ min (т/м2) | τ max (т/м2) | ε1 min | ε1 max | ε2 min | ε2 max | ε3 min | ε3 max |
1 | -41.175 | 2776.7 | -1228.2 | 609.49 | -5559 | 20.309 | 103.08 | 2758.9 | 1.60E-05 | 8.66E-04 | -5.32E-05 | 1.07E-04 | -1.73E-03 | -6.49E-05 |
2 | -25.949 | 3109.5 | -1180.1 | 584.53 | -6224.8 | -22.588 | 115.62 | 3134.9 | 1.76E-05 | 9.79E-04 | -6.24E-05 | 1.18E-04 | -1.96E-03 | -7.31E-05 |
3 | -54.522 | 3453 | -1191.3 | 589.84 | -6911.7 | -45.335 | 128.23 | 3501.9 | 1.93E-05 | 1.09E-03 | -7.28E-05 | 1.33E-04 | -2.19E-03 | -8.03E-05 |
Поврежденные объемные конечные элементы. |
1 | -98.783 | 1851.3 | -1346.7 | 668.16 | -3442.1 | 48.756 | 61.302 | 1671.7 | 2.96E-05 | 1.64E-03 | -6.02E-04 | 2.97E-04 | -2.97E-03 | -1.09E-04 |
2 | -28.817 | 2072.2 | -1227.3 | 607.2 | -3810.7 | 26.163 | 68.833 | 1910.2 | 3.28E-05 | 1.86E-03 | -4.41E-04 | 2.24E-04 | -3.37E-03 | -1.23E-04 |
3 | -11.518 | 2267 | -1224.1 | 605.74 | -4137.6 | -8.4975 | 75.55 | 2118.8 | 3.63E-05 | 2.05E-03 | -3.93E-04 | 2.35E-04 | -3.69E-03 | -1.35E-04 |
Таблица 2. Главные напряжения и соответствующие им деформации при статическом нагружении
Не поврежденные объемные конечные элементы |
№ | σ1 (т/м2) | σ2 (т/м2) | σ3 (т/м2) | τ (т/м2) | ε1 | ε2 | ε3 |
1 | -0.041 | -38.324 | -206.200 | 103.080 | 1.60E-05 | 9.55E-07 | -6.49E-05 |
2 | -0.200 | -39.237 | -231.450 | 115.620 | 1.76E-05 | 2.32E-06 | -7.31E-05 |
3 | -0.244 | -39.835 | -256.690 | 128.230 | 1.93E-05 | 3.78E-06 | -8.13E-05 |
Поврежденные объемные конечные элементы |
№ | σ1 (т/м2) | σ2 (т/м2) | σ3 (т/м2) | τ (т/м2) | ε1 | ε2 | ε3 |
1 | -1.890 | -42.039 | -124.490 | 61.302 | 2.96E-05 | -1.58E-05 | -1.09E-04 |
2 | -1.141 | -40.666 | -138.810 | 68.833 | 3.28E-05 | -1.20E-05 | -1.23E-04 |
3 | 0.254 | -40.431 | -150.850 | 75.550 | 3.63E-05 | -9.73E-06 | -1.35E-04 |
Сравнив действующие максимальные и минимальные главные напряжения и соответствующие им деформации в статической и динамической постановке, можно сделать вывод, что возникающие деформации в коррозионно-поврежденных объемных конечных элементах больше, чем в неповрежденных, несмотря на то что некоторые из действующих главных напряжений в этих же КЭ меньше.
Для объемных конечных элементов №4-7 (рис.8) в таблице 3 и 4 приведены главные напряжения, и деформации в динамической и статической постановке соответственно. КЭ приняты неповрежденными, но определение максимальных и минимальных главных напряжений, и соответствующих им деформаций сформированы из поврежденной и не поврежденной железобетонной балки.
Таблица 3. Главные напряжения и соответствующие им деформации при динамическом нагружении
Не поврежденный железобетонный элемент |
№ | σ1 min (т/м2) | σ1 max (т/м2) | σ2 min (т/м2) | σ2 max (т/м2) | σ3 min (т/м2) | σ3 max (т/м2) | τ min (т/м2) | τ max (т/м2) | ε1 min | ε1 max | ε2 min | ε2 max | ε3 min | ε3 max |
4 | -139.86 | 42709 | -291.42 | 589.33 | -21121 | 282.36 | 788.5 | 21213 | 7.9E-05 | 2.1E-03 | -6.2E-04 | 3.0E-04 | -1.0E-03 | -2.4E-05 |
5 | 84.162 | 3460.5 | -1.0248 | 0.5058 | -1751.9 | -6.3074 | 67.455 | 1844 | 4.2E-05 | 1.1E-03 | -2.1E-04 | 1.1E-04 | -5.8E-04 | -1.0E-05 |
6 | -11.179 | 869.97 | -558.32 | 277.8 | -897.05 | 5.5436 | 13.213 | 631.21 | 3.1E-06 | 3.1E-04 | -1.3E-04 | 6.3E-05 | -3.1E-04 | -7.3E-06 |
7 | -8.1326 | 1574.7 | -1076.7 | 535.19 | -3000.9 | 4.0369 | 56.293 | 1496.4 | 9.4E-06 | 4.9E-04 | -1.6E-04 | 7.6E-05 | -9.1E-04 | -3.5E-05 |
Поврежденный железобетонный элемент |
№ | σ1 min (т/м2) | σ1 max (т/м2) | σ2 min (т/м2) | σ2 max (т/м2) | σ3 min (т/м2) | σ3 max (т/м2) | τ min (т/м2) | τ max (т/м2) | ε1 min | ε1 max | ε2 min | ε2 max | ε3 min | ε3 max |
4 | -178.7 | 49837 | -362.31 | 687.1 | -26231 | 346.07 | 908.51 | 24745 | 9.1E-05 | 2.5E-03 | -7.2E-04 | 3.8E-04 | -1.3E-03 | -2.7E-05 |
5 | 49.507 | 3691.4 | -2.9247 | 1.4506 | -1975.2 | -11.564 | 73.565 | 2032.6 | 4.5E-05 | 1.2E-03 | -2.2E-04 | 1.2E-04 | -6.6E-04 | -1.3E-05 |
6 | -17.309 | 1152 | -1069.6 | 532.53 | -1764.5 | 8.696 | 32.665 | 873.59 | 6.5E-06 | 3.5E-04 | -2.3E-04 | 1.2E-04 | -5.1E-04 | -1.9E-05 |
7 | -0.603 | 2788.3 | -1461.3 | 727.67 | -5220.3 | 0.3066 | 96.325 | 2609.9 | 1.6E-05 | 8.8E-04 | -1.4E-04 | 9.1E-05 | -1.6E-03 | -6.0E-05 |
Таблица 4. Главные напряжения и соответствующие им деформации при статическом нагружении
Не поврежденный железобетонный элемент |
№ | σ1 (т/м2) | σ2 (т/м2) | σ3 (т/м2) | τ (т/м2) | ε2 | ε3 | σ1 (т/м2) |
4 | 1587.2 | 21.985 | 10.215 | 788.5 | 7.89E-05 | -2.3E-05 | -2.4E-05 |
5 | 128.6 | -0.03697 | -6.3074 | 67.455 | 4.24E-05 | -8E-06 | -1E-05 |
6 | 0.028957 | -20.85 | -26.397 | 13.213 | 3.1E-06 | -5.1E-06 | -7.3E-06 |
7 | -0.00548 | -31.703 | -112.59 | 56.293 | 9.43E-06 | -3E-06 | -3.5E-05 |
Поврежденный железобетонный элемент |
№ | σ1 (т/м2) | σ2 (т/м2) | σ3 (т/м2) | τ (т/м2) | ε2 | ε3 | σ1 (т/м2) |
4 | 1829.4 | 25.304 | 12.43 | 908.51 | 9.09E-05 | -2.6E-05 | -2.7E-05 |
5 | 135.57 | -0.08293 | -11.564 | 73.565 | 4.51E-05 | -8.1E-06 | -1.3E-05 |
6 | -0.07985 | -34.519 | -65.409 | 32.665 | 6.51E-06 | -7E-06 | -1.9E-05 |
7 | 0.1967 | -44.557 | -192.45 | 96.325 | 1.56E-05 | -2E-06 | -6E-05 |
Сопоставив данные таблиц 3 и 4, определено, что максимальные и минимальные главные напряжения и соответствующие им деформации возникают в неповрежденных объемных конечных элементах, коррозионно-поврежденной балки. Это объясняется тем, что прочностные характеристики коррозионно–поврежденных конечных элементов снижены относительно первоначальных, вследствие чего действующие напряжения от внешней нагрузки перераспределяются на сопряженные элементы, увеличивая их численно.
Кроме возникающих напряжений и деформаций от внешних нагрузок, появляются перемещения узлов по локальным осям Z, X, Y. На рисунках 10 и 11 представлены общие перемещения по оси Z от динамического нагружения, неповреждённого и коррозионно-поврежденного железобетонного элемента, соответственно.

Рисунок 10. Перемещение по оси Z коррозионно–поврежденной железобетонной балки
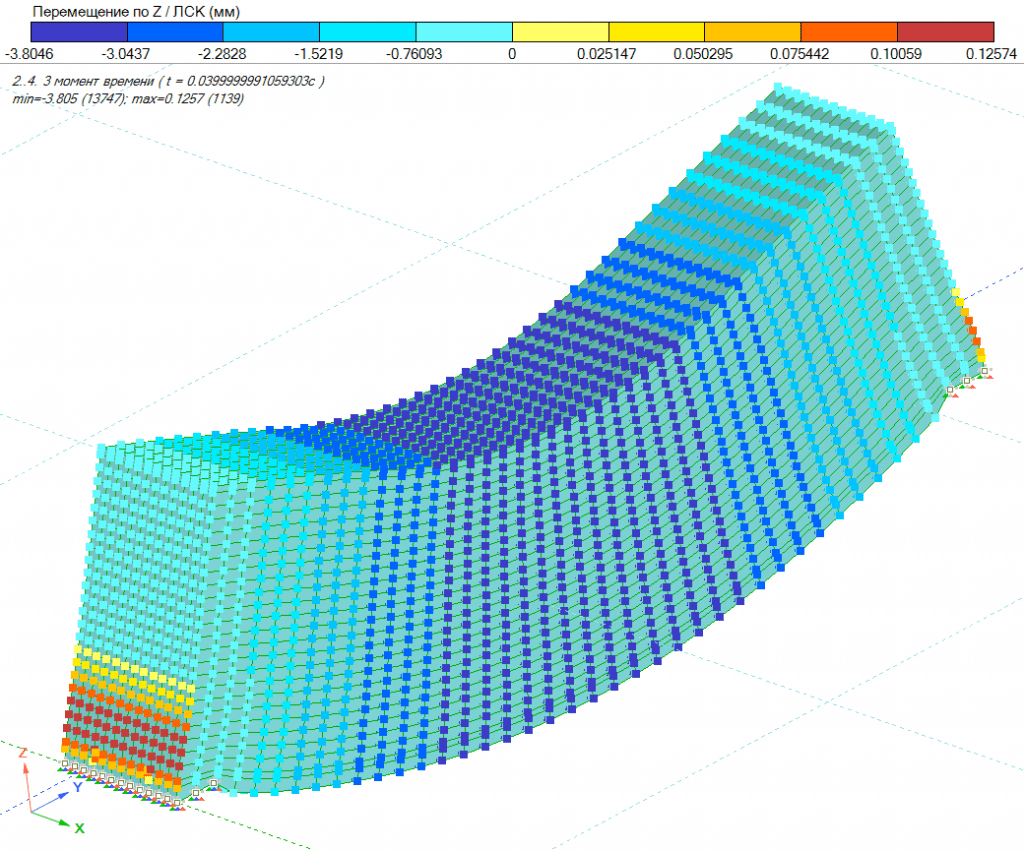
Рисунок 11. Перемещение по оси Z неповрежденной железобетонной балки
Максимальные перемещения узлов по оси Z возникают на 0,066 секунде, перемещения узлов коррозионно-поврежденного элемента численно больше на 0,8мм, что в процентном отношении составляет 17%. Причиной больших перемещений является меньшая жесткость коррозионно-поврежденной балки.
Таким образом, выводами по результатам расчета в программном комплексе, коррозионно–поврежденной и неповрежденной балки из объемных восьмиузловых конечных элементов являются:
В коррозионно-поврежденной балке напряжения в растянутой зоне больше, а напряжения в сжатой зоне меньше, чем в не поврежденной балке;
Увеличивается риск хрупкого разрушения коррозионно-поврежденного элемента, вследствие увеличения высоты сжатой зоны бетона;
В коррозионно–поврежденных КЭ при динамическом и статическом нагружении, возникающие деформации больше чем в неповрежденных, даже при условии, что некоторые из действующих главных напряжений в этих же КЭ меньше;
За счет перераспределения усилий в не поврежденных КЭ коррозионно–поврежденной балки, возникающие напряжения и соответствующие им деформации больше, чем в неповрежденной балке.
ЛИТЕРАТУРА:
Ларионова Е.А. Влияние коррозии на диссипацию энергии при силовом деформировании // Вестник МГСУ, № 6. С. 26-34, 2016
Тамразян А.Г. Рекомендации к разработке требований к живучести зданий и сооружений // Вестник МГСУ, № 2. С. 77-83, 2011
Тамразян А.Г, Орлова М.А. К остаточной несущей способности железобетонных балок с трещинами // Жилищное строительство, №6, С.32-34, 2015.
Тамразян, А.Г. Бетон и железобетон – взгляд в будущее / А.Г. Тамразян // Вестник МГСУ, № 4. С. 181–189, 2014.
Бондаренко В.М., Клюева Н.В., Пискунов А.В. Прикладная диссипативная теория конструктивной безопасности железобетона// Известия Орел ГТУ, серия строительство, транспорт, № 1/21 (553), С. 8-19, 2009.
Бондаренко В.М. Специфика силового сопротивления поврежденных коррозией железобетонных конструкций и новые факторы разрушения // Известия Орел ГТУ, серия строительство, транспорт, № 4, С. 28-33, 2009.
СП 63.13330.2012. Бетонные и железобетонные конструкции.