Журнал: Сейсмостойкое строительство. Безопасность сооружений. 2016. №5
Рубрика: ТЕОРЕТИЧЕСКИЕ И ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
Автор(ы): Булушев С.В., Джинчвелашвили Г.А., Колесников А.В.
Аннотация:
Нелинейный статический метод или Pushover Analysis, широко используемый за рубежом, основан на методе спектра несущей способности. В работе подробно описан метода нелинейного статического анализа с учетом возможности использования в отечественной нормативной литературе. Выполнен анализ гипотез и допущений при расчете на сейсмические воздействия сооружений нелинейным статическим методом, который позволяет проектировать простые и регулярные здания и сооружения с заданным уровнем обеспеченности сейсмостойкости на основе критерия необрушения несущих конструкций. Процедура нелинейного статического метода проанализирована на примере простой системы. Полученная сходимость результатов расчета на сейсмические воздействия зданий и сооружений на рассмотренном примере показала достоверность реализации автоматизированного расчета нелинейным статическим методом в ПК ЛИРА 10.4.
Нелинейный статический метод анализа сейсмостойкости зданий и сооружений (Pushover Analysis)
Введение
Обеспечение надежности и безопасности сейсмостойкого строительства, несомненно, представляет собой сложнейшую инженерную задачу. Нормами проектирования, разработанными в последнее время, допускается возможность работы материала конструкций за пределами упругости. Предполагается нелинейное поведение конструкций, и даже допускаются разрушения отдельных несущих элементов, которые должны быть относительно легкодоступны для обследования, ремонта и разрушение которых не наносит большого ущерба конструкции в целом [8].
Перед проектировщиками стоит задача рассчитать сооружения таким образом, чтобы при сильных землетрясениях разрушения не превышали определенного уровня, т.е. были бы контролируемыми и приемлемыми [4].
Расчет конструкций с учетом нелинейного поведения при разрушении отдельных элементов сооружения требует использования более сложных математических моделей и теорий [1 – 7, 15 – 18, 20 - 25].
В настоящее время в российских нормах по сейсмостойкому строительству до сих пор используется линейно-спектральный метод [8]. Этот метод достаточно прост и может достаточно точно оценить реакцию системы, работающей в упругой стадии, на сейсмическое воздействие. Но по мере перехода системы в неупругую стадию работы, точность оценки снижается. Слабая обоснованность коэффициента К1может сильно занизить реакцию системы, допускающей пластические деформации [1, 4 и др.].
В связи с этим, появляется необходимость в использовании методов, которые учитывают нелинейную работу материалов и конструкций в целом. Одним из таких методов является нелинейный динамический анализ [1 – 7]. Но из-за своей трудоемкости, он не может быть закреплен в нормах, как основной для зданий и сооружений с низкой степенью ответственности.
За рубежом, при расчете сейсмостойкости зданий и сооружений, в практике проектирования, наряду со спектральным методом, применяется нелинейный статический метод, который в свою очередь основан на энергетических критериях [2, 12 – 15, 17 – 19, 21 - 23]. Этот метод получил название «Nonlinear Pushover analysis», а принятый в нём подход к проектированию можно рассматривать как проектирование сейсмостойких конструкций с заданными параметрами сейсмостойкости. Вектор поперечной силы F, используемый в этом методе определяется по формуле:
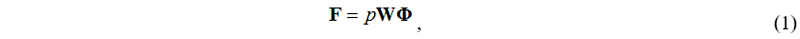
где p параметр, контролирующий величину поперечной силы; W матрица масс; Ф – матрица форм собственных колебаний.
Существенным допущением является то, что рассматривается система дифференциальных уравнений, в которой учитываются только горизонтальные степени свободы:
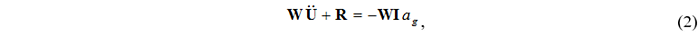
где U и R векторы перемещений и внутренних сил, соответственно; I единичный вектор; ag ускорение грунта основания, как функция времени.
Отметим, что диссипативные силы в выражении (2) отсутствуют. Они уже включены в расчетный спектр ускорений. Считается, что форма колебания Ф остается постоянной, то есть, что она не меняется в процессе колебания сооружения при движении основания. Это основное и самое важное предположение в рамках процедуры нелинейного статического анализа.
Наиболее известный метод нелинейного статического анализа - метод спектра несущей способности (Capacity Spectrum Method, CSM). Этот метод впервые был предложен Фрименом [18, 23], а затем утвержден в ATC-40 [12]. Сейчас в американских нормах используется модифицированный метод спектра несущей способности [13].
Хотя этот метод широко используется за рубежом, в русскоязычной литературе он встречается довольно редко [2, 3, 4]. А если и встречается, то описан недостаточно подробно, что затрудняет возможность использования данного метода в инженерной практике.
Целью настоящей работы является:
- подробно описать методологию нелинейного статического анализа с учетом возможности использования в реалиях российских норм;
- рассмотреть применение метода на примере простой системы;
- оценить полученные результаты;
- оценить возможность применения метода в инженерной практике.
Методика расчета состоит из этапов.
1. Создание расчетной модели. Расчет на сейсмические воздействия необходимо производить с учетом геометрической и физической нелинейностей. Диаграммы деформирования конструктивных элементов следует принимать в соответствии с указаниями [11] для железобетонных конструкций и приложению В [9] для стальных конструкций.
2. Приложение статических вертикальных нагрузок согласно п. 5.1 [8] и п. 6.2 6.3 [10].
3. Приложение боковой нагрузки согласно одному из вариантов распределения по высоте сооружения:
• равномерное распределение:
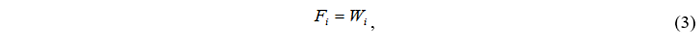
где Wi масса i-го этажа;
• распределение по j-ой форме колебаний:
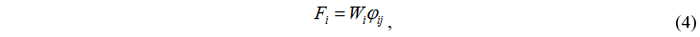
где
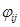
перемещение
i-го этажа по
j-ой форме;
• распределение по обратному треугольнику:
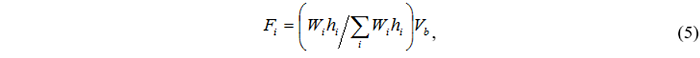
где высота i-го этажа, поперечная сила в основании, полученная линейно-спектральным методом;
• распределение согласно распределению сейсмических сил по п. 5.5-5.10 [8].
4. Постепенно увеличивая боковую нагрузку до достижения верхом сооружения предельных перемещений или до полного обрушения конструкции (что становится возможным при учете физической нелинейности), получаем зависимость поперечной силы в основании от перемещения верха сооружения - кривую несущей способности. При этом необходимо учитывать появление текучести в элементах от комбинации вертикальной и боковой нагрузки (рис. 1).
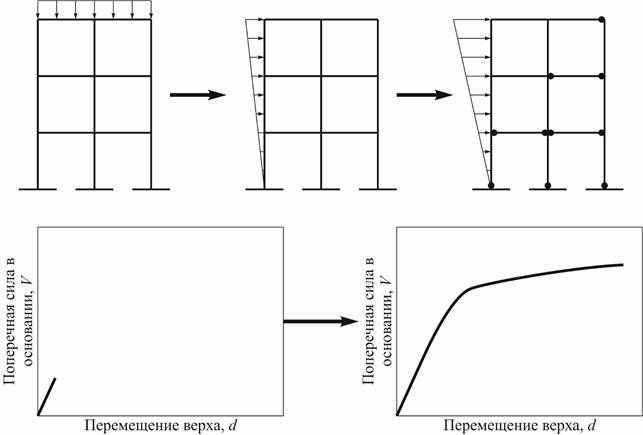
Рисунок 1. Построение кривой несущей способности сооружения
5. Преобразование кривой несущей способности в спектр несущей способности с помощью следующих соотношений, в зависимости от направления сейсмического воздействия [12, 13] (рис. 2).:
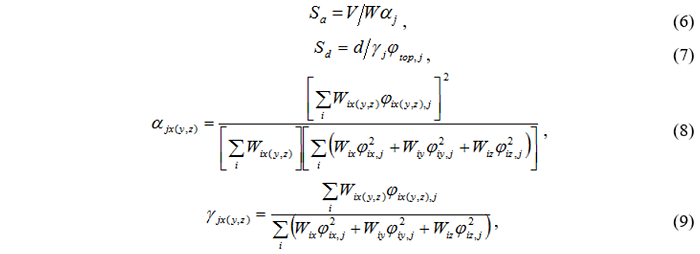
где V поперечная сила в основании, W масса всего сооружения, d перемещение верха сооружения, 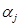 коэффициент модальной массы j-ой формы,
коэффициент модальной массы j-ой формы, 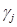 коэффициент распределения j-ой формы.
коэффициент распределения j-ой формы.
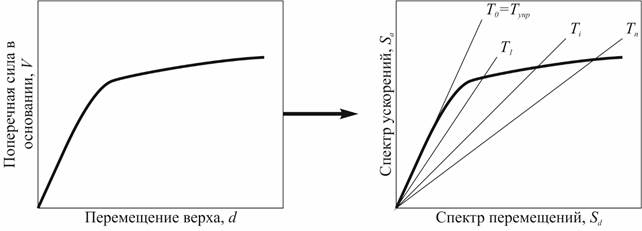
Рисунок 2. Преобразование кривой несущей способности в спектр несущей способности
6. Расчетный спектр отклика необходимо перевести в формат «Спектр ускорений - Спектр перемещений» или другими словами Спектр Реакций в формате Ускорения-Перемещения (СРУП). В зарубежной литературе Acceleration-Displacement Response Spectrum, ADRS (рис. 3):
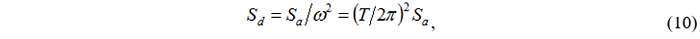
Спектр ускорений согласно п. 5.5 5.6 [8] получаем следующим образом:
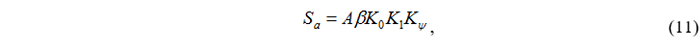
K1 в данном случае принимаем равным 1.
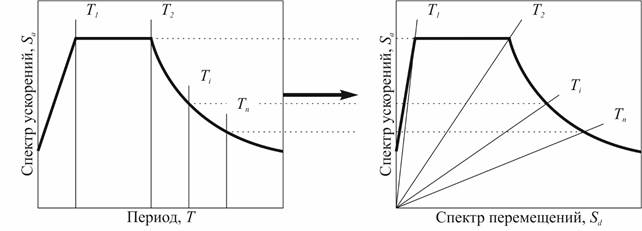
Рисунок 3. Преобразование расчетного спектра в формат СРУП
7. Полученные спектры наносятся совместно в координатах «Спектр ускорений Спектр перемещений» (рис. 4).
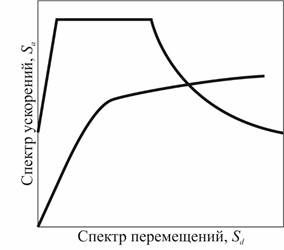
Рисунок 4. Совмещение полученных спектров
8. Выбираем предполагаемую характеристическую точку (максимальное ускорение
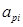
и максимальное перемещение
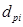
). Выбор точки может быть основан на принципе эквивалентных перемещений, как показано на рисунке 5, либо на любом другом предположении.
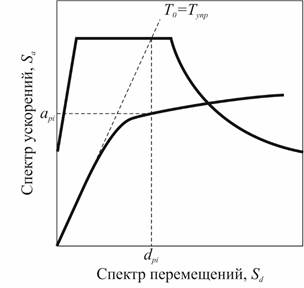
Рисунок 5. Выбор предполагаемой характеристической точки
9. Производим билинейную аппроксимацию спектра несущей способности исходя из условия равенства площадей A1 = A2 (рис 6). Тем самым получаем перемещение точки текучести 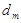 и ускорение точки текучести
и ускорение точки текучести 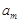 .
.
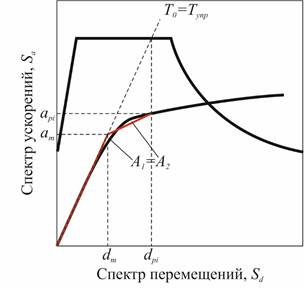
Рисунок 6. Билинейная аппроксимация спектра несущей способности
10. Исходя из полученной билинейной аппроксимации получаем значения коэффициента пост-упругой жесткости и коэффициента пластичности по следующим формулам:
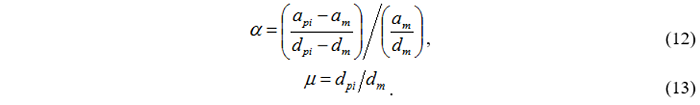
11. Используя коэффициенты пост-упругой жесткости α и пластичности μ, определяем эффективное затухание 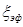 и эффективный период
и эффективный период 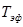 :
:
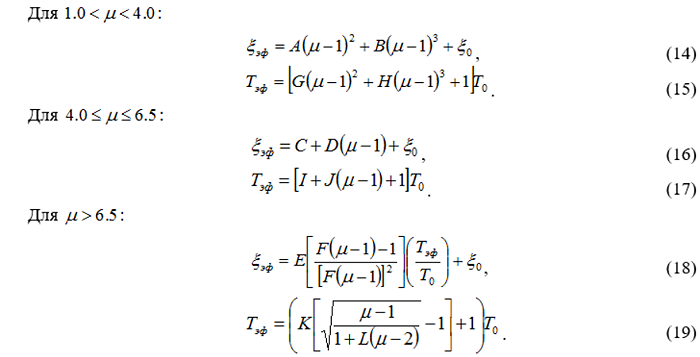
Коэффициенты для конструкций, которые работают по билинейному гистерезису, могут быть определены из таблиц (табл. 1, 2) в зависимости от коэффициента пост-упругой жесткости . При определении промежуточных значений допускается определять по линейной интерполяции.
В дальнейшем для нахождения решения может быть использовано несколько алгоритмов [13].
Алгоритм А.
12.А Для полученного эффективного затухания 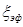 строим новый спектр реакции
строим новый спектр реакции  с помощью следующего соотношения:
с помощью следующего соотношения:

13.A Величина максимального перемещения di системы определяется точкой пересечения эффективного периода Tэф и СРУП. Величина максимального ускорения ai находится из точки на спектре несущей способности, соответствующей di.
14.A Если полученная характеристическая точка 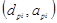 совпадает с предполагаемой характеристической точкой или находится в достаточной близости (порядка 5%), то это и есть искомые величины максимального ускорения и перемещения системы. Если нет, тогда необходимо повторить все шаги, начиная с шага 8, выбрав новую точку
совпадает с предполагаемой характеристической точкой или находится в достаточной близости (порядка 5%), то это и есть искомые величины максимального ускорения и перемещения системы. Если нет, тогда необходимо повторить все шаги, начиная с шага 8, выбрав новую точку 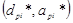 (рис. 7).
(рис. 7).
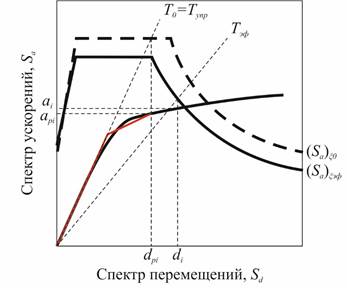
Рисунок 7. Нахождение характеристической точки по алгоритму А
Алгоритм Б.
12.Б Для полученного эффективного затухания 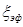 строим новый спектр реакции (18) , (19).
строим новый спектр реакции (18) , (19).
13.Б Умножая только ординаты нового спектра на коэффициент М, получаем модифицированный спектр отклика в формате «Спектр ускорений - Спектр перемещений» или Модифицированный Спектр Реакций Ускорения – Перемещения (МСРУП). В зарубежной литературе Modified Acceleration-Displacement Response Spectrum (MADRS). Коэффициент преобразования находится, используя начальный , эффективный и секущий периоды системы:
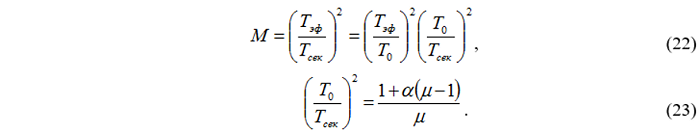
14.Б Величины максимального ускорения ai и перемещения di системы определяются точкой пересечения спектра несущей способности и МСРУП.
15.Б Если полученная характеристическая точка 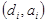 совпадает с предполагаемой характеристической точкой
совпадает с предполагаемой характеристической точкой 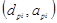 или находится в достаточной близости (порядка 5%), то это и есть искомые величины максимального ускорения и перемещения системы. Если нет, тогда необходимо повторить все шаги, начиная с шага 8, выбрав новую точку
или находится в достаточной близости (порядка 5%), то это и есть искомые величины максимального ускорения и перемещения системы. Если нет, тогда необходимо повторить все шаги, начиная с шага 8, выбрав новую точку 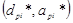 (рис. 8).
(рис. 8).
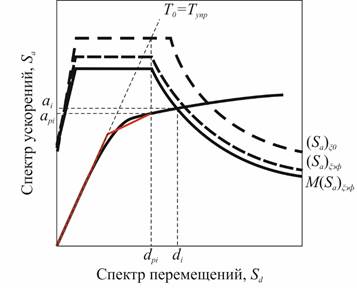
Рисунок 8. Нахождение характеристической точки по алгоритму Б
Алгоритм В.
12.В Для полученного эффективного затухания 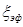 строим новый спектр реакции (18) , (19).
строим новый спектр реакции (18) , (19).
13.В Умножая ординаты нового спектра на коэффициент М (20) (21), получаем модифицированный спектр отклика в формате МСРУП (MADRS).
14.В Возможная характеристическая точка определяется пересечением прямой секущего периода 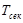 и МСРУП.
и МСРУП.
15.В Выбирая различные точки 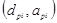 , и повторяя шаги, начиная с шага 8, получаем серию возможных характеристических точек.
, и повторяя шаги, начиная с шага 8, получаем серию возможных характеристических точек.
16.В Искомая характеристическая точка пересечения кривой, полученной в предыдущем шаге, и спектра несущей способности (рис. 9).
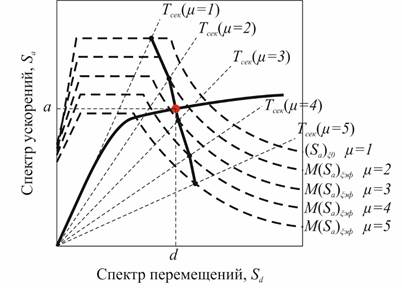
Рисунок 9. Нахождение характеристической точки по алгоритму В
17.B Выполняя обратный переход к кривой несущей способности  ,
,  , (4) – (7), получаем перемещение рассматриваемой точки и поперечную силу в основании системы.
, (4) – (7), получаем перемещение рассматриваемой точки и поперечную силу в основании системы.
Далее кратко рассмотрим применение данной методики на примере стальной одноэтажной плоской рамы типового производственного здания (рис. 10). Перекрытие принято абсолютно жестким.
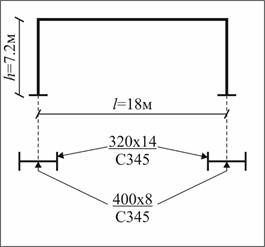
Рисунок 10. Расчетная схема
Расчет производился в программном комплексе ЛИРА 10.4 и системе компьютерной математики Matlab.
Приведем решение задачи в виде алгоритма.
1. Рассчитываем раму на сейсмическое воздействие по [8] в ПК ЛИРА 10.4. Получаем сейсмические силы по первой форме.
2. Прикладываем полученные силы в качестве нагрузок и производим расчет на сейсмические воздействия в нелинейной статической постановке. Диаграмма деформирования приведена на рис. 11. В результате получаем кривую несущей способности.
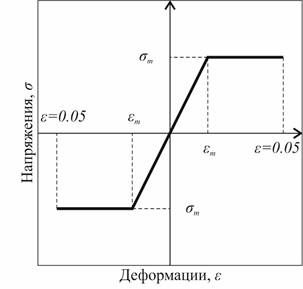
Рисунок 11. Диаграмма деформирования стали
3. Выполняя шаги 5 и 11 вышеописанной методики, получаем эффективное затухание 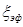 и эффективный период
и эффективный период 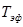 (рис. 12). Дальнейший расчет на сейсмические воздействия осуществляется по алгоритму А.
(рис. 12). Дальнейший расчет на сейсмические воздействия осуществляется по алгоритму А.
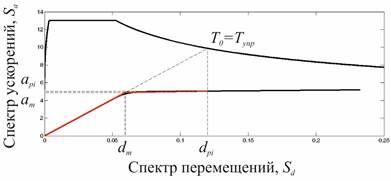
Рисунок 12. Применение методики. Шаги 5 11
4. Результаты выполнения шагов 12.А и 14.А приведены на рис. 13. Так как точки 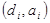 и
и 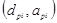 не находятся в достаточной близости, повторяем все итерации, начиная с шага 8. Новая точка
не находятся в достаточной близости, повторяем все итерации, начиная с шага 8. Новая точка 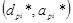 выбиралась посередине между точками
выбиралась посередине между точками 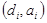 и
и 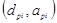 .
.
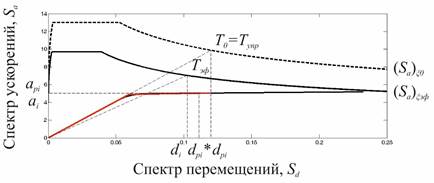
Рисунок 13. Применение методики. Шаги 12.А 14.А
5. Выполнив 9 итераций, получаем, что точки совпали с точностью 0.1% (рис. 14).
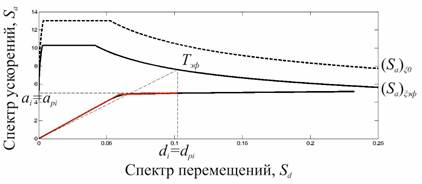
Рисунок 14. Применение методики. Окончательный результат
6. Определив перемещение рассматриваемой точки, переходим к соответствующему шагу нелинейного расчета в ПК ЛИРА 10.4. Таким образом, получаем напряженно-деформированное состояние системы.
7. Так же, с помощью данной методики можно определить коэффициент 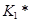 , соответствующий данной расчетной схеме сооружения. Из рисунка 15 видно, что полученный коэффициент
, соответствующий данной расчетной схеме сооружения. Из рисунка 15 видно, что полученный коэффициент 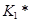 существенно отличается от коэффициента
существенно отличается от коэффициента 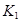 [8].
[8].
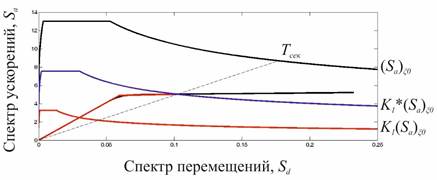
Рисунок 15. Расчетные спектры реакции: исходный, с полученным коэффициентом 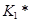 и с коэффициентом
и с коэффициентом 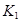 [8]
[8]
Рассмотрим решение вышеописанной задачи с использованием модуля Pushover analysis, реализованного в ПК ЛИРА 10.4 (Рис. 16):
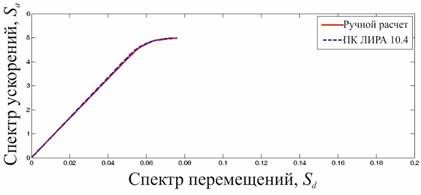
Рисунок 16. Сравнение «ручного расчета» с модулем Pushover analysis в ПК ЛИРА 10.4
Полученная сходимость результатов расчета сейсмостойкости зданий и сооружений позволяет судить о достоверности реализации автоматизированного расчета нелинейным статическим методом (Pushover analysis) в ПК ЛИРА 10.4 в рамках рассмотренного примера.
Скачать пример задачи с использованием Pushover analysis в ПК ЛИРА 10.4
Заключение
1. В условиях неопределенности сейсмологической информации, для анализа несущей способности сооружений при сейсмических воздействиях достаточно продуктивным оказался энергетический критерий – критерий равенства энергий.
2. В практике проектирования, наряду со спектральным методом, должен применяться нелинейный статический метод, который в свою очередь основан на энергетических критериях. Этот метод получил название «Nonlinear Pushover analysis», а принятый в нём подход к проектированию можно рассматривать как проектирование сейсмостойких конструкций с заданными параметрами сейсмостойкости.
3. Методика нелинейного статического анализа в расчете сейсмостойкости зданий и сооружений в зависимости от постановки позволяет, либо отказаться от коэффициента 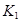 совсем (как показано выше), либо вычислять коэффициент
совсем (как показано выше), либо вычислять коэффициент 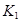 для конкретного здания или сооружения не прибегая к таблице 4 [8]. Такой подход позволяет с большей точностью оценивать реакцию систем определенной конструктивной схемы, допускающей повреждения и пластические деформации, на сейсмическое воздействие.
для конкретного здания или сооружения не прибегая к таблице 4 [8]. Такой подход позволяет с большей точностью оценивать реакцию систем определенной конструктивной схемы, допускающей повреждения и пластические деформации, на сейсмическое воздействие.
4. Согласно п. 5.2.б [8], при расчете на сейсмические воздействия, соответствующие уровню МРЗ, необходимо учитывать возможность развития неупругих деформаций. При решении задачи в такой постановке применение нелинейного статического метода не запрещается и может применяться широким кругом специалистов.
5. Рассмотренный в настоящей работе «ручной» метод определения кривой СРУП и характеристической точки может быть применен с использованием любого отечественного или зарубежного программного комплекса, позволяющего производить статические расчеты с учетом физической и геометрической нелинейностей. Это позволяет применять рассмотренный метод в инженерной практике.
6. В работе выполнен анализ гипотез и допущений при расчете сооружений на землетрясения нелинейным статическим методом, который позволяет проектировать простые и регулярные здания и сооружения с заданным уровнем сейсмостойкости на основе критерия необрушения несущих конструкций.
7. Этот метод весьма эффективен для зданий и сооружений со стальным и железобетонным каркасом (в том числе, связевым) простой формы, с регулярным распределением несущих элементов в плане и по вертикали. Однако, для зданий перекрестно-стеновой конструктивной системы, он дает большие погрешности по сравнению с нелинейными динамическими методами. Более сложные конструктивные схемы зданий и сооружений будут рассмотрены в следующих работах.
В ЛИРА 10.6, презентация которой состоится 6 декабря в Москве, расчет на сейсмические воздействия с использованием нелинейного статического метода (Pushover analysis) был существенно модернизирован.
Подробнее о презентации
Список литературы:
1. Джинчвелашвили Г. А., Мкртычев О.В. Оценка нелинейной работы зданий и сооружений при аварийных воздействиях // Проблемы безопасности российского общества. 2012. №3. - с. 17-31.
2. Джинчвелашвили Г. А. Нелинейные динамические методы расчета зданий и сооружений с заданной обеспеченностью сейсмостойкости //автореферат дисс. на соискание ученой степени докт. техн. наук. – М.: МГСУ, 2015. – 46 с.
3. Задоян П.М. Оценка сейсмостойкости методом спектра несущей способности. // Известия Ереванского государственного университета архитектуры и строительства, 2/2009.
4. Мкртычев О.В., Джинчвелашвили Г. А. Проблемы учета нелинейностей в теории сейсмостойкости (гипотезы и заблуждения) // Москва: МГСУ, 2012. (Библиотека научных разработок и проектов МГСУ). - 192 с.
5. Мкртычев О.В., Джинчвелашвили Г.А., Бусалова М.С. Задача вероятностного расчета конструкции на нелинейно деформируемом основании со случайными параметрами // Вестник МГСУ. 2013. № 12. - с. 106-112.
6. Мкртычев О.В., Джинчвелашвили Г.А., Дзержинский Р.И. Философия многоуровневого проектирования в свете обеспечения сейсмостойкости сооружений // Геология и геофизика Юга России. 2016. № 1. - с. 71-81.
7. Мкртычев О.В., Джинчвелашвили Г.А. Оценка работы зданий и сооружений за пределами упругости при сейсмических воздействиях // XXI Russian-Slovak-Polish Seminar, “Theoretical Foundation of Civil Engineering”, Moscow-Archangelsk 03.07 – 06.07.2012. - pp. 177 – 186.
8. СП 14.13330.2014. «Строительство в сейсмических районах. Актуализированная редакция СНиП II-7-81*», М., 2014;
9. СП 16.13330.2011. «Стальные конструкции. Актуализированная редакция СНиП II-23-81*», М., 2011;
10. СП 20.13330.2011. «Нагрузки и воздействия. Актуализированная редакция СНиП 2.01.07-85*», М., 2011;
11. СП 63.13330.2012. «Бетонные и железобетонные конструкции. Основные положения. Актуализированная редакция СНиП 52-01-2003» М., 2012;
12. Applied Technology Council (ATC). «Seismic Evaluation and Retrofit of Concrete Buildings». Rep. No. ATC-40, Volumes 1 and 2, Redwood City, CА, 1996.
13. Applied Technology Council (ATC). «Improvement of nonlinear static seismic analysis procedures». Rep. No. ATC-55, Redwood City, CА, 2005.
14. Building Seismic Safety Council. NEHRP Guidelines for the Seismic Rehabilitation of Buildings, FEMA-273, Federal Emergency Management Agency, Washington, DC, 1997.
15. Chopra Anil K. Dynamics of Structures. Theory and Applications to Earthquake Engineering. – Prentice Hall, Inc. 1995, Englewood Cliffs, New Jersey, 07632. – 794 p.
16. Clough Ray W., Penzien Joseph. Dynamics of Structures (Third Edition). - Computers & Structures, Inc. 1995 University Ave., Berkeley, CA 94704, USA. – 752 p.
17. Datta T. K. Seismic Analysis of Structures, John Wiley & Sons (Asia) Pte Ltd. 2010. – p. 464.
18. Freeman S.A., «Prediction of Response of Concrete Buildings to Severe Earthquake Motion», Douglas McHenry International Symposium on Concrete and Concrete Structures, SP-55, American Concrete Institute, Detroit, Michigan, 1978. Pp. 589-605.
19. Kanai K. Semi-empirical formula for the seismic characteristics of the ground. BERJ, 35 (1957).
20. Mkrtychev O.V., Dzhinchvelashvili G.A., Busalova M.S. Calculation accelerograms parameters for a ”Construction-Basis” model, nonlinear properties of the soil taken into account / Procedia Engineering –2014 - vol.91, pp. 54-57.
21. NEHRP Recommended Provisions for Seismic Regulations for New Buildings and other Structures. Part 1: 1997 Edition. Building Seismic Safety Council (USA), - 342p.
22. Paz Mario. Structural Dynamics: Theory and Computation / by Mario Paz, William Leigh. – 5th ed., 2004. – 844p.
23. Themelis S. Pushover analysis for seismic assessment and design of structures, Heriot-Watt University, School of Built Enviroment, 2008;
24. Verruijt Arnold. SOIL DYNAMICS /Delft University of Technology 1994, 2008. – 425p.
25. Wolf J.P. Dynamic Soil-Structure Interaction /1985, Prentice-Hall, Inc., Englewood Cliffs, N.J. 07632. – 481 p.