Подбор и проверка металлических конструкций в ПК ЛИРА 10.4 имеет ряд преимуществ и особенностей. Разберем подробно тонкости расчёта конструирования металлических конструкций.
В ПК ЛИРА 10.4 реализована функция автоматического определения характера работы элемента. В процессе расчёта производится внутрипрограммный выбор характера работы элементов стальных конструкций (центральное растяжение-сжатие; сжатие-растяжение с изгибом вокруг одной или двух главных осей; изгиб в одном или в двух главных направлениях). Данная функция программы освобождает пользователя от анализа работы элемента и, таким образом, снижает вероятность допущения ошибки, поскольку один и тот же элемент при различных комбинациях загружений может работать по-разному. Выбор производится в зависимости от соотношения действующих в рассматриваемом сечении усилий, которое определяется величиной относительного или приведенного относительного эксцентриситета (таблица 1).
Таблица 1.
| N < 0 (присутствует сжатие) | N > 0 (присутствует растяжение) |
| Приведенный относительный эксцентриситет для сжатой грани mef y(z) | Характер работы относительно рассматриваемой оси | Относительный эксцентриситет для растянутой грани m y(z) | Характер работы относительно рассматриваемой оси |
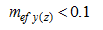 | Сжатие | 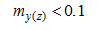 | Растяжение |
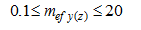 | Сжатие с изгибом |  | Растяжение с изгибом |
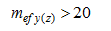 | Изгиб | 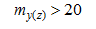 | Изгиб
|
В настоящей версии программы выполняются следующие проверки стальных конструкций, в качестве нормативного документа будем рассматривать СП 16.13330.2011.
Первое предельное состояние
Прочность Таблица 2.
| Проверки прочности | Обозначение | Формулы проверок |
| СП 16.13330.2011 |
| Прочность по нормальным напряжениям: | | (106) – без учёта стеснённого кручения.
(105) – без учёта стеснённого кручения. |
| – без учёта развития пластических деформаций | 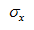 |
| – с учётом развития пластических деформаций | 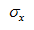 |
| Прочность несимметричных сечений из высокопрочной стали по нормальным напряжениям растяжения | 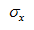 | (107) |
| Прочность по касательным напряжениям | 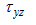 | (42) |
| Прочность по приведенным напряжениям (совместное действие нормальных и касательных напряжений) |  | (44)
|
- Прочность по нормальным напряжениям может проверяться с учётом, или без учёта развития пластических деформаций. Возможность учёта развития пластических деформаций задаётя пользователем в параметрах конструирования. При этом можно руководствоваться разд. 8.1. Следует отметить, что в настоящей редакции СП 16.13330.2011, в связи с отсутствием коэффициентов учёта пластики для полного пластического шарнира, конструкции 3 класса по виду напряжённого состояния (полный пластический шарнир) считаются так же, как и конструкции 2 класса (ограниченное развитие пластики).
В случае допустимости расчета с учетом развития пластических деформаций программой выполняется проверка фактического наличия пластики. Для этого выполняются две проверки:
- проверка 1 – с учетом развития пластических деформаций;
- проверка 2 – без учета развития пластических деформаций.
Если прочность по проверке 1 обеспечивается, а по проверке 2 – нет, то элемент в данном сечении действительно работает с учетом развития пластических деформаций. И только в этом случае производится учет пластики в дальнейших проверках устойчивости и местной устойчивости.
Формулы для проверки прочности по нормальным напряжениям, указанные в таблице 2 и используемые в программе, учитывают все составляющие усилий в рассматриваемом сечении.
- Прочность по касательным напряжениям проверяется по формулам (42) в основе которых лежит формула Журавского.
- Прочность по приведенным напряжениям (совместное действие нормальных и касательных напряжений) проверяется по формулам теории прочности (44).
Общая устойчивость
Таблица 3.
Проверки общей устойчивости
| Обозначение
| Формулы проверок
|
СП 16.13330.2011
|
| Устойчивость плоской формы изгиба | 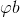
| (70) – без учёта стеснённого кручения.
|
| Устойчивость по изгибной форме | 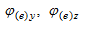
| (109), (120), (121)
|
| Устойчивость по изгибно-крутильной форме | 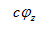
| (111)
|
| Устойчивость стержней, подверженных сжатию и изгибу в двух главных плоскостях | 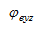
| (116)
|
- Устойчивость плоской формы изгиба
Проверка устойчивости плоской формы изгиба (по φb) производится для открытых профилей следующих типов: двутавр симметричный, двутавр несимметричный, тавр, швеллер, а также для полосы. При определении коэффициента устойчивости при изгибе φb используется расчётная длина lef b, которая задаётся пользователем по указаниям пунктов 8.4.2 и часто равна расчётной длине элемента в плоскости минимальной жёсткости. Коэффициент φb определяется в соответствии с указаниями приложения Ж. Все задаваемые исходные данные соответствуют таблицам указанных приложений. Если заранее известно, что для рассматриваемого конструктивного элемента такая проверка не понадобится или вид нагрузки и загруженный пояс определить невозможно (например, колонна каркаса здания), рекомендуется для симметричных двутавров и швеллеров задать балочную схему работы, два и более боковых закреплений, а для несимметричных двутавров и тавров задать вид нагрузки, вызывающий чистый изгиб.
Для сечений из несимметричных двутавров или тавров в программе отсутствует проверка устойчивости плоской формы изгиба для консолей, по причине отсутствия указаний для такой проверки консолей в действующих нормах.
Поскольку для сечений из полосы в нормах отсутствуют указания для проверки устойчивости плоской формы изгиба, в программе определение коэффициента устойчивости при изгибе φb производится по формулам (Ж.1), (Ж.2).
- Устойчивость по изгибной форме.
Важным вопросом при выполнении этой проверки является определение расчётных длин элементов. Расчётные длины задаются пользователем. При этом он может руководствоваться разделом 10, или специальной литературой (например, С. Д. Лейтес «Справочник по определению свободных длин элементов стальных конструкций», Москва, 1963 г).
Для сечений из одиночного уголка пользователь должен задать радиус инерции, используемый для данной проверки. При этом следует руководствоваться п. 10.1.4, 10.2.2 и 10.2.3.
Следует отметить, что в соответствии со всеми рассматриваемыми нормами коэффициент продольного изгиба при внецентренном сжатии 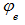 не может быть больше коэффициента продольного изгиба при центральном сжатии
не может быть больше коэффициента продольного изгиба при центральном сжатии 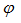 (см. примечание п. 2 к таблице коэффициентов
(см. примечание п. 2 к таблице коэффициентов 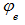 в рассматриваемых нормах). Поэтому проверка устойчивости центрально сжатых элементов рассматривается как частный случай проверки устойчивости по изгибной форме сжато-изогнутых элементов.
в рассматриваемых нормах). Поэтому проверка устойчивости центрально сжатых элементов рассматривается как частный случай проверки устойчивости по изгибной форме сжато-изогнутых элементов.
Для коробчатых сечений и для сечений из сплошного прямоугольника (полосы) обозначение 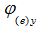 соответствует проверке по формулам (121), соответственно обозначение
соответствует проверке по формулам (121), соответственно обозначение 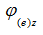 – по формулам (120).
– по формулам (120).
Для сечения из одиночного швеллера при наличии изгиба в плоскости большей жёсткости значения коэффициента формы сечения 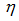 принимаются как для симметричного двутавра, о чём выводится соответствующее предупреждение.
принимаются как для симметричного двутавра, о чём выводится соответствующее предупреждение.
Для несимметричных двутавров общего вида с произвольным соотношением площадей большей и меньшей полок, в нормах отсутствуют значения коэффициента формы сечения 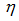
. В программе коэффициент 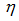 определяется с помощью кубической интерполяции между приведенными в нормах типами сечений. Параметром для интерполяции служит коэффициент
определяется с помощью кубической интерполяции между приведенными в нормах типами сечений. Параметром для интерполяции служит коэффициент 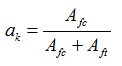 (осевой коэффициент асимметрии несимметричного двутавра), где Afc и Аft соответственно площадь сжатой и растянутой полки.
(осевой коэффициент асимметрии несимметричного двутавра), где Afc и Аft соответственно площадь сжатой и растянутой полки.
В программе определяется значение коэффициента 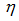 для каждого из перечисленных типов сечений, после чего между этими данными производится кубическая интерполяция по фактическому значению аk рассматриваемого профиля. Об этом выводится соответствующее предупреждение.
для каждого из перечисленных типов сечений, после чего между этими данными производится кубическая интерполяция по фактическому значению аk рассматриваемого профиля. Об этом выводится соответствующее предупреждение.
Для сечений из круглой трубы или сплошного круглого сечения при проверке устойчивости по изгибной форме:
- если расчётные длины элемента в обеих плоскостях равны, т. е. если
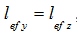 , используется результирующий момент, равный геометрической сумме моментов в двух взаимно-перпендикулярных направлениях:
, используется результирующий момент, равный геометрической сумме моментов в двух взаимно-перпендикулярных направлениях: 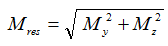 ;
; - если
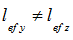 , выполняются две независимые проверки: относительно оси Y1 с использованием момента Му и расчётной длины
, выполняются две независимые проверки: относительно оси Y1 с использованием момента Му и расчётной длины 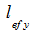 , и относительно оси Z1 с использованием момента Мz и расчётной длины
, и относительно оси Z1 с использованием момента Мz и расчётной длины 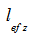 .
.
- Устойчивость по изгибно-крутильной форме
Проверка производится по формулам (111.
Для сечения из одиночного швеллера при наличии изгиба в плоскости большей жёсткости значения коэффициентов α и β принимаются как для симметричного двутавра, о чём выводится соответствующее предупреждение.
При относительных эксцентриситетах в плоскости большей жёсткости 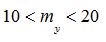 параметр с определяется по формуле (43) полученной из условия
параметр с определяется по формуле (43) полученной из условия 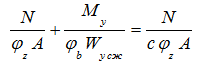 (имеется в виду, что плоскость большей жёсткости X10Z1). При этом, в соответствии с указаниями п. 9.2.4 [9.11коэффициент φb, входящий в эту формулу определяется как для балки с двумя и более боковыми закреплениями, независимо от заданных пользователем.
(имеется в виду, что плоскость большей жёсткости X10Z1). При этом, в соответствии с указаниями п. 9.2.4 [9.11коэффициент φb, входящий в эту формулу определяется как для балки с двумя и более боковыми закреплениями, независимо от заданных пользователем.
Программой предусмотрена проверка устойчивости также и для растянуто-изогнутых элементов. Проверка производится на основании формулы
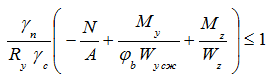 (1)
(1)
Сила растяжения в этом случае оказывает разгружающее действие, но это не гарантирует устойчивость сжатого пояса элемента.
Для сечения из полосы 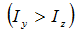 в нормах нет указаний для проверки устойчивости по изгибно-крутильной форме. Коэффициент с к формуле (111) определяется по формуле (2), полученной из условия (3
в нормах нет указаний для проверки устойчивости по изгибно-крутильной форме. Коэффициент с к формуле (111) определяется по формуле (2), полученной из условия (3
)
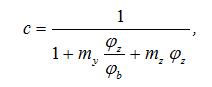 (2)
(2)
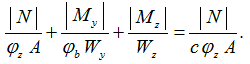 (3)
(3)
При проверке местной устойчивости стенок учёт локальных напряжений не предусмотрен. Предполагается также отсутствие продольных рёбер жёсткости. Наличие и шаг поперечных рёбер жёсткости задаёт пользователь, руководствуясь п. 8.5.9, п. 9.4.4. Для изгибаемых элементов отсутствие поперечных рёбер жёсткости приводит к увеличению толщины стенки, которая в этом случае проверяется из условия 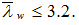 по требованию п. 8.5.9. В то же время программа не контролирует необходимость постановки поперечных рёбер жёсткости для сжатых и сжато-изогнутых элементов по п. 9.4.4, поскольку эти требования являются конструктивными и не влияют на расчёт.
по требованию п. 8.5.9. В то же время программа не контролирует необходимость постановки поперечных рёбер жёсткости для сжатых и сжато-изогнутых элементов по п. 9.4.4, поскольку эти требования являются конструктивными и не влияют на расчёт.
При проверке местной устойчивости коробчатых сечений, в общем случае, при наличии изгибающих моментов в обоих главных направлениях (Му ≠ 0, Мz ≠ 0), необходимо определить, какие из граней коробки считать стенками, а какие полками.
Таблица 4.
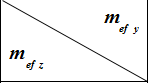 | 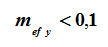 | 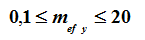 | 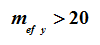 |
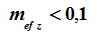 | Центральное сжатие. Стенками считаются все 4 стороны | Внецентренное сжатие вокруг оси Y1. Стенками считаются стороны, параллельные Z1 | Изгиб вокруг оси Y1. Стенками считаются стороны, параллельные оси Z1 |
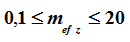 | Внецентренное сжатие вокруг оси Z1. Стенками считаются стороны, параллельные оси Y1 | Внецентренное сжатие в двух направлениях. Стенками считаются стороны, параллельные оси Z1 | Стенками считаются стороны, параллельные оси Z1 |
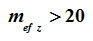 | Изгиб вокруг оси Z1. Стенками считаются стороны, параллельные оси Y1 | Стенками считаются стороны, параллельные оси Y1 | Изгиб в двух направлениях. Стенками считаются стороны, параллельные оси Z1 |
Второе предельное состояние
Прогибы
Прогибы элементов или конструктивных элементов проверяются в направлении их локальных осей Y1 и Z1. Необходимость такой проверки при подборе или проверке стальных конструкций задаётся пользователем на основании приложения Е СП 20.13330.2011 или других нормативных документов. При этом используются нормативные (эксплуатационные) значения постоянных нагрузок и длительные нагрузки, или длительно действующая часть кратковременных нагрузок со своими коэффициентами сочетаний. Такой подход справедлив для конструкций, загруженных постоянными, полезными, снеговыми и другими нагрузками, имеющими длительно действующую часть. К таким конструкциям относятся, например, стропильные балки, ригели покрытия, прогоны покрытия, балки и ригели перекрытий, балки рабочих и обслуживающих площадок, лестничные косоуры и марши, балки балконов и лоджий. Опоры конструктивных элементов (места, где прогибы принимаются равными нулю) задаются с помощью раскреплений. Если заданы раскрепления конструктивного элемента, то его прогиб считается относительно прямой линии, соединяющей эти раскрепления. При отсутствии раскреплений принимается полное перемещение сечений конструктивного элемента в составе расчётной схемы. Необходимость задания раскреплений определяет пользователь. Следует обратить внимание, что в режиме подбора сечения конструктивного элемента принято, что величина его прогиба изменяется обратно пропорционально изгибной жёсткости ЕI рассматриваемого конструктивного элемента и не учитывает перемещение других элементов расчётной схемы. Если при наличии раскреплений это предположение справедливо, то при их отсутствии такой подход может привести к неправильному результату. Поэтому в случае обоснованного отсутствия раскреплений окончательный расчёт сечений должен быть выполнен в режиме проверки.
Предельно допустимые прогибы задаются пользователем. При этом в каждом из направлений он может задать как величину прогиба в миллиметрах или в долях пролёта, так и автоматический выбор предельного прогиба по п. 2 таблицы Е.1 СП 20.13330.2011.
Для конструкций, у которых ограничены горизонтальные прогибы и перемещения от ветра по п. Е.2.4.1, Е.2.4.3, Е.2.4.4 СП 20.13330.2011 следует выполнить дополнительную проверку таких прогибов по локальным эпюрам перемещений, либо проверку горизонтальных перемещений соответствующих узлов от нормативных (эксплуатационных) значений ветровых нагрузок. К таким конструкциям относятся, например, колонны каркаса, стойки фахверка, ригели фахверка, опоры конвейерных галерей.
Проверку прогибов сложных стержневых систем, например, стропильных ферм или структурных блоков покрытия, следует выполнять по перемещениям характерных узлов в различных комбинациях загружений (с помощью РСН).
Гибкость
Необходимость такой проверки задаётся пользователем. Проверка гибкости конструктивных элементов производится на основании п. 10.4.1, 10.4.2 СП 16.13330.2011. Величину предельно допустимой гибкости задаёт пользователь. При этом он может задать требуемую величину сам, либо воспользоваться подсказкой программы, выбрав нужную строку из предлагаемых таблиц действующих норм.
Следите за нашими новостями и задавайте вопросы на форуме.