Данная заметка нацелена прежде всего на начинающих расчётчиков, у которых часто возникают вопросы, как выбрать размер сетки конечных элементов, в каких случаях она является качественной, а в каких нет и т.д. Но, возможно, и более опытные пользователи ПК ЛИРА 10 найдут в ней полезные вещи.
Процесс разбиения модели на конечные элементы (КЭ) называется триангуляцией. Совокупность КЭ, на которые разбита конструкция, называется, конечно, элементной сеткой. Триангуляция является одним из ключевых этапов создания расчетной схемы в ПК ЛИРА 10. От корректности разбиения на КЭ зависит точность результатов расчета. К основным видам КЭ относят:
- одноузловые;
- стержневые;
- пластинчатые;
- объемные.
К двум основным типам сетки КЭ относятся регулярные и нерегулярные.
Регулярные сетки представляют собой совокупность КЭ правильной геометрии (рис. 1).
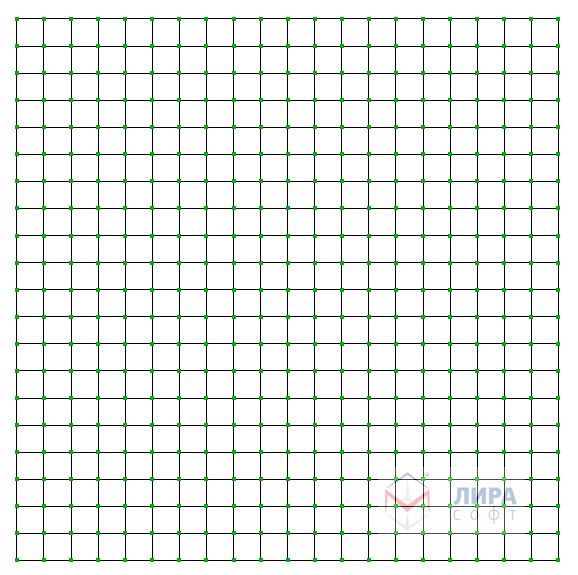
Рис. 1. Упорядоченная сетка КЭ
Для нерегулярной сетки размеры соседних элементов (h) могут существенно различаться, и сетка не имеет четкой структуры (рис. 2).
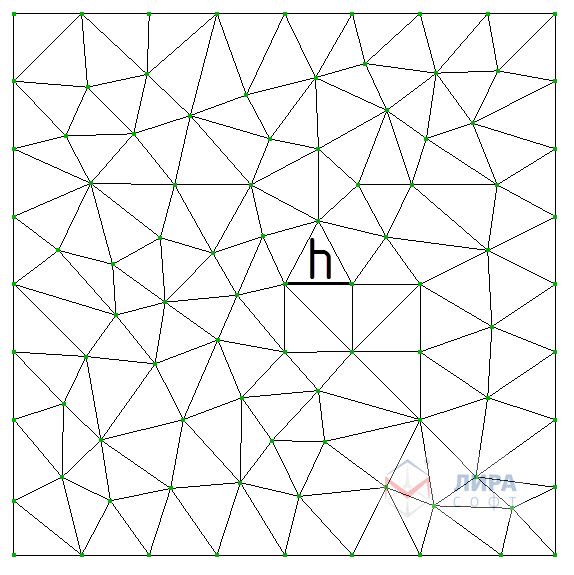
Рис. 2. Произвольная сеть КЭ
При выборе типа и размера сетки конечных элементов рекомендуем руководствоваться следующими принципами, которые помогут получить максимально близкие к реальности результаты:
- регулярная сетка дает более точные результаты, чем нерегулярная;
- прямоугольные 4-узловые КЭ дают более точные результаты, чем треугольные;
- треугольные элементы с промежуточными узлами имеют точность, близкую к сетке прямоугольных 4-х узловых элементов;
- прямоугольная сетка с промежуточными узлами дает более точные результаты, чем треугольная сетка с промежуточными узлами, несмотря на большую площадь;
- промежутки между КЭ не допускаются;
- допускается комбинация треугольных и четырехугольных элементов в одной модели;
- строить 4-узловые элементы с тупым (>180°) внутренним углом запрещается.
Количество элементов в расчётной модели обратно пропорционально размеру конечных элементов h, при этом, время расчета увеличивается по экспоненте с уменьшением размеров КЭ (рис. 3).
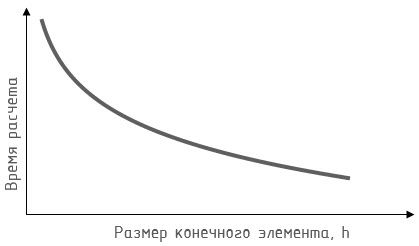
Рис. 3. График зависимости времени расчёта от размеров КЭ
При выборе размеров сетки конечных элементов необходимо всегда помнить, что сам метод конечных элементов – это метод числового приближения, и абсолютной точности он дать не может. Да, погрешность вычислений снижается при уменьшении размеров КЭ, но полностью она не устраниться, и, зачастую, дальнейшее уменьшение сети не будет приводить к ощутимому увеличению точности, но время расчёта будет возрастать, этот момент нужно держать в голове и не стремиться к слишком мелкой сетке.
Для примера рассмотрим модель прямоугольной консольной плиты (рис. 4).
Геометрия:

Рис. 4. Пример
Исходные данные:
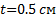 ;
; 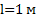 ;
; 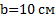
Характеристики материала:
Изотропный упругий: 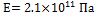 ,
, 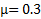
Граничные условия:
Контур плиты вдоль оси Y жёстко заделан.
Нагрузка:
Распределённая нагрузка по площади плиты: 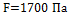
Описание задачи:
Плита моделировалась КЭ 42,44 – тонкой оболочки.
На рисунке 5 и в таблице демонстрируются изменения величины перемещения по Z в зависимости от размера КЭ. Одну и ту же модель прямоугольной консольной плиты рассчитали трижды, меняя лишь максимальный размер КЭ. Сравнивая результаты, полученные при аналитическом расчете с результатами расчета в ПК ЛИРА 10.8, видим, что наиболее точные значения получаются при расчете с меньшим шагом сетки.
Результаты расчёта:
Искомая Величина | Аналитическое решение | Результаты расчёта ЛИРА 10.8 | Отклонение, % |
Шаг сетки | Значение |
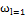 , м , м | -0,0973 | 0,2 | -0,09495 | 2,415 |
0,1 | -0,09571 | 1,634 |
0,05 | -0,095815 | 1,526 |
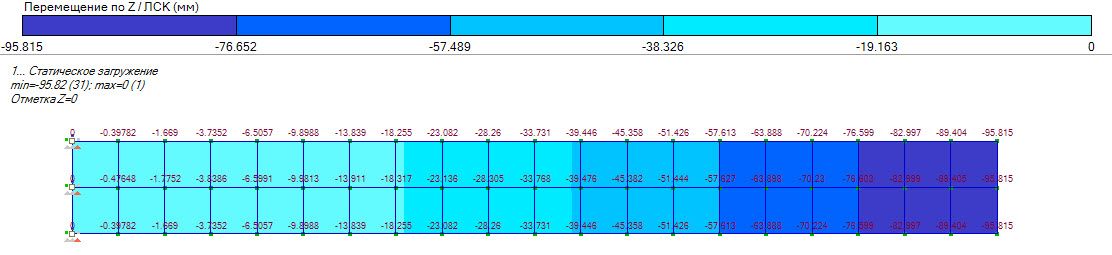
Рис. 5. Результаты расчётов
Более мелкая сетка особенно важна там, где есть изменения напряжений и деформаций (изменяются на порядок). Крупная сетка КЭ может использоваться в областях постоянного напряжения или зонах, которые не интересуют пользователя. При этом расчётчик должен четко понимать, где какая зона находится. Более мелкая сетка может потребоваться в местах стыка нескольких несущих элементов, у отверстий, в углах, зонах контакта и в областях с высоким напряжением (рис. 6).
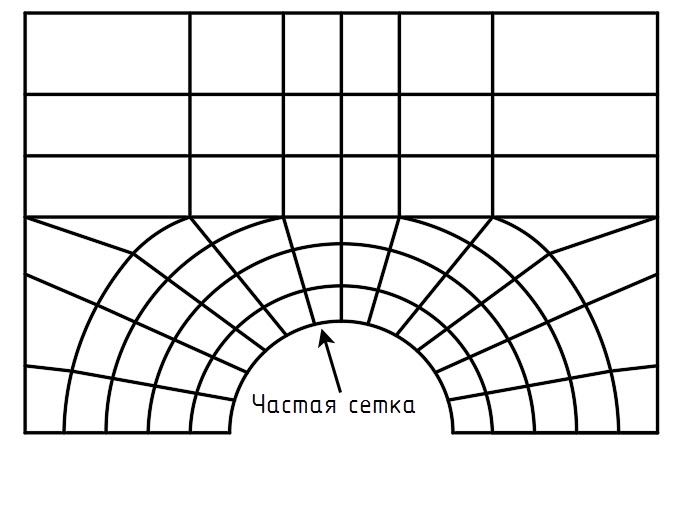
Рис. 6. Область сгущения сетки КЭ
В то же время, необходимо учитывать тот факт, что точность уменьшается, если размеры соседних элементов около концентраторов напряжений сильно различаются. Это связано с тем, что матрица жесткостей становится плохо обусловленной. Ко всему вышесказанному следует добавить следующее: отношение максимального размера элемента к минимальному не должно превышать 2, или угол не должен быть меньше 30° (рис.7).
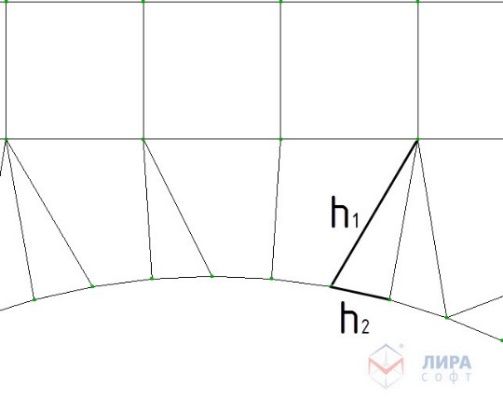
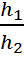 ≤2
≤2
Рис. 7. Выбор формы КЭ
Форма конечных элементов значительно влияет на точность. При создании расчётных моделей рекомендуется избегать появление острых углов в КЭ, наибольшую точность дают элементы с одинаковыми сторонами или близкими к одинаковым (рис. 8).
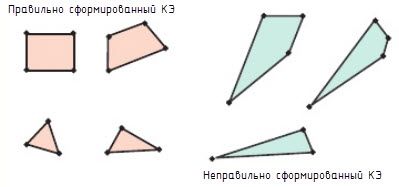
Рис. 8. Выбор формы КЭ
Точных рекомендаций относительно идеального размера пластинчатых КЭ не существует, но отталкиваться следует от размеров 1:10 пролета и не превышать размера в 1000 мм.
При отношении толщины КЭ к его длине и ширине более 1:5 следует использовать объёмные элементы.
Список использованных источников и литературы
- Бате К., Вилсон Е. Численные методы анализа и метод конечных элементов / Пер. с англ. А. С. Алексеева и др.; Под ред. А. Ф. Смирнова. – М.: Стройиздат, 1982 – 448 с., ил. – Перевод изд.: Numerical methods in finite element analysis /K.-J. Bathe, E.L. Wilson (1976).
- Городецкий А. С., И. Д. Евзеров. Компьютерные модели конструкций: издательство «Факт», 2005. – 344 с.
- Scribd [Электронный ресурс]. – URL: https://ru.scribd.com/doc/19184786/How-to-Design-r-c-Flat-Slabs-Using-Finite-Element-Analysis. – How to design reinforced concrete flat slabs using Finite Element Analysis. – (Дата обращения: 29.11.2017).
- Шимановский А. О. Применение метода конечных элементов в решении задач прикладной механики: учеб. - метод. Пособие для студентов технических специальностей /, А. О. Шимановский, А. В. Путято; М-во образования Респ. Беларусь, Белорус. гос. ун-т трансп. – Гомель: БелГУТ, 2008. – 61с.
- Расчет и проектирование конструкций высотных зданий из монолитного железобетона / А. С. Городецкий [и др.]: издательство «Факт», 2004. – 106 с.